
【题目】如图,A,B,C,D为平面四边形ABCD的四个内角. 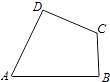
(1)证明:tan ![]() =
= ![]() ;
;
(2)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() 的值.
的值.
【答案】
(1)证明: tan ![]() =
= ![]() =
= 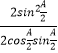 =
= ![]() .等式成立.
.等式成立.
(2)解:由A+C=180°,得C=180°﹣A,D=180°﹣B,由(Ⅰ)可知:tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() =
= ![]() =
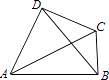
= ![]() ,连结BD,在△ABD中,有BD2=AB2+AD2﹣2ABADcosA,AB=6,BC=3,CD=4,AD=5,
,连结BD,在△ABD中,有BD2=AB2+AD2﹣2ABADcosA,AB=6,BC=3,CD=4,AD=5,
在△BCD中,有BD2=BC2+CD2﹣2BCCDcosC,
所以AB2+AD2﹣2ABADcosA=BC2+CD2﹣2BCCDcosC,
则:cosA= ![]() =
= ![]() =
= ![]() .
.
于是sinA= ![]() =
= ![]() ,
,
连结AC,同理可得:cosB= ![]() =
= ![]() =
= ![]() ,
,
于是sinB= ![]() =
= ![]() .
.
所以tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)直接利用切化弦以及二倍角公式化简证明即可.(2)通过A+C=180°,得C=180°﹣A,D=180°﹣B,利用(1)化简tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() =
= ![]() ,连结BD,在△ABD中,利用余弦定理求出sinA,连结AC,求出sinB,然后求解即可.
,连结BD,在△ABD中,利用余弦定理求出sinA,连结AC,求出sinB,然后求解即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数 ![]() .
.
(1)用含a的式子表示b;
(2)令F(x)= ![]() ,其图象上任意一点P(x0 , y0)处切线的斜率
,其图象上任意一点P(x0 , y0)处切线的斜率 ![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若a=2,试求f(x)在区间 ![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线方程为![]() ,问:是否存在过点M(1,1)的直线l,使得直线与双曲线交于P,Q两点,且M是线段PQ的中点?如果存在,求出直线的方程,如果不存在,请说明理由.
,问:是否存在过点M(1,1)的直线l,使得直线与双曲线交于P,Q两点,且M是线段PQ的中点?如果存在,求出直线的方程,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
(a>0,且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是_____________.
①.如果命题“![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,那么命题
”都是真命题,那么命题![]() 一定是真命题.
一定是真命题.
②.命题![]() ,则
,则![]()
③.命题“若![]() ,则
,则![]() ”的否命题是:“若
”的否命题是:“若![]() ,则
,则![]() ”
”
④.特称命题 “![]() ,使
,使![]() ”是真命题.
”是真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某广场中间有一块边长为2百米的菱形状绿化区ABCD,其中BMN是半径为1百米的扇形,∠ABC= ![]() .管理部门欲在该地从M到D修建小路:在
.管理部门欲在该地从M到D修建小路:在 ![]() 上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ.
上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ. 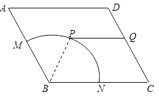
(1)若∠PBC= ![]() ,求PQ的长度;
,求PQ的长度;
(2)当点P选择在何处时,才能使得修建的小路 ![]() 与PQ及QD的总长最小?并说明理由.
与PQ及QD的总长最小?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在其定义域内存在
在其定义域内存在![]() ,使得
,使得![]() 成立,则称函数
成立,则称函数![]() 为“可分拆函数”.
为“可分拆函数”.
(1)试判断函数![]() 是否为“可分拆函数”?并说明你的理由;
是否为“可分拆函数”?并说明你的理由;
(2)设函数![]() 为“可分拆函数”,求实数
为“可分拆函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com