
如图,两个工厂A、B相距2km,点O为AB的中点,要在以O为圆心,2km为半径的圆弧MN上的某一点P处建一幢办公楼,其中MA⊥AB,NB⊥AB.据测算此办公楼受工厂A的“噪音影响度”与距离AP的平方成反比,比例系数为1;办公楼受工厂B的“噪音影响度”与距离BP的平方也成反比,比例系数为4,办公楼与A、B两厂的“总噪音影响度”y是A、B两厂“噪音影响度”的和,设AP为xkm.

(1)求“总噪音影响度”y关于x的函数关系式,并求出该函数的定义域;
(2)当AP为多少时,“总噪音影响度”最小?
(1)y= (
( ≤x≤
≤x≤ )(2)AP=
)(2)AP= km
km
【解析】(1)(解法1)如图,连结OP,

设∠AOP=α,则 ≤α≤
≤α≤ .
.
在△AOP中,由余弦定理得x2=12+22-2×1×2cosα=5-4cosα,
在△BOP中,由余弦定理得BP2=12+22-2×1×2cos(π-α)=5+4cosα,
∴BP2=10-x2,∴y= .
.
∵ ≤α≤
≤α≤ ,∴
,∴ ≤x≤
≤x≤ ,∴y=
,∴y= (
( ≤x≤
≤x≤ ).
).

(解法2)建立如图所示的直角坐标系,则A(-1,0),B(1,0),设P(m,n),则PA2=(m+1)2+n2,PB2=(m-1)2+n2.
∵m2+n2=4,PA=x,
∴PB2=10-x2(后面解法过程同解法1).
(2)(解法1)y= =
= [x2+(10-x2)]
[x2+(10-x2)]
= (5+
(5+ )≥
)≥ (5+2
(5+2 )=
)= ,
,
当且仅当 ,即x=
,即x= ∈[
∈[ ,
, ]时取等号.
]时取等号.
故当AP= km时,“总噪音影响度”最小.
km时,“总噪音影响度”最小.
(解法2)由y= ,得
,得
y′=- .
.
∵ ≤x≤
≤x≤ ,∴令y′=0,得x=
,∴令y′=0,得x= ,且当x∈
,且当x∈ 时,y′<0;当x∈(
时,y′<0;当x∈( ,
, ]时,y′>0.∴x=
]时,y′>0.∴x= 时,y=
时,y= 取极小值,也即最小值.故当AP=
取极小值,也即最小值.故当AP= km时,“总噪音影响度”最小
km时,“总噪音影响度”最小


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第3课时练习卷(解析版) 题型:解答题
已知函数f(x)=2x- ,x∈(0,1].
,x∈(0,1].
(1)当a=-1时,求函数y=f(x)的值域;
(2)若函数y=f(x)在x∈(0,1]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:解答题
已知函数f(x)=lnx-ax2+(2-a)x.
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x< 时,f
时,f >f
>f ;
;
(3)若函数y=f(x)的图象与x轴交于A、B两点,线段AB中点的横坐标为x0,证明: <0.
<0.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
若函数f(x)=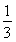 x3-
x3-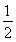 ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.
ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
某公司为一家制冷设备厂设计生产某种型号的长方形薄板,其周长为4m.这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后AB′交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB′PD的面积最大时制冷效果最好.
(1)设AB=xm,用x表示图中DP的长度,并写出x的取值范围;
(2)若要求最节能,应怎样设计薄板的长和宽?
(3)若要求制冷效果最好,应怎样设计薄板的长和宽?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:解答题
设在海拔xm处的大气压强是yPa,y与x之间的函数关系为y=cekx,其中c、k为常量.已知某天的海平面的大气压为1.01×105Pa,1000m高空的大气压为0.90×105Pa,求600m高空的大气压强.(保留3位有效数字)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:解答题
已知函数f(x)=(ax2+x)ex,其中e是自然数的底数,a∈R.
(1)当a<0时,解不等式f(x)>0;
(2)若f(x)在[-1,1]上是单调函数,求a的取值范围;
(3)当a=0时,求整数k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:填空题
已知函数f(x)=-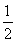 x2+blnx在区间[
x2+blnx在区间[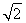 ,+∞)上是减函数,则b的取值范围是________.
,+∞)上是减函数,则b的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第10课时练习卷(解析版) 题型:填空题
若一次函数f(x)=ax+b有一个零点2,那么函数g(x)=bx2-ax的零点是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com