
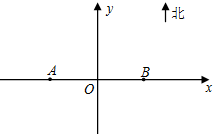
 为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.
为了监测某海域的船舶航行情况,在该海域设立了如图所示东西走向,相距20海里的A,B两个观测站,观测范围是到A,B两观测站距离之和不超过40海里的区域.| 2 |
| 3 |
 解:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系.…(1分)
解:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系.…(1分)| x2 |
| a2 |
| y2 |
| b2 |
|
| 3 |
| x2 |
| 400 |
| y2 |
| 300 |
|
| 20 |
| 7 |
| 2 |
| 20 |
| 7 |
| 120 |
| 7 |
| 2 |
| 24 |
| 8 |


科目:高中数学 来源: 题型:
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:
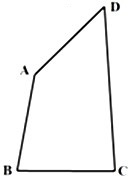 如图,在凸四边形ABCD中,C,D为定点,CD=
如图,在凸四边形ABCD中,C,D为定点,CD=| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 2 |
| 3 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com