练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求函数z=1-
    1-x2
    4-x
    的值域．
    考点：函数的值域
    专题：函数的性质及应用
    分析：根据二次根式
    1-x2
    4-x
    ≥0，考查
    1-x2
    4-x
    的取值范围，即可得出函数的值域．
    解答： 解：∵函数z=1-
    1-x2
    4-x
    ，
    ∴
    1-x2
    4-x
    ≥0，
    即
    1-x2
    4-x
    ≥0，
    ∴
    (x+1)(x-1)
    x-4
    ≥0，
    解得-1≤x≤1，或x＞4；
    ∴当x∈{x|-1≤x≤1，或x＞4}时，函数的值域是（-∞，1]．
    点评：本题考查了求函数值域的问题，解题的关键是利用二次根式的意义解答，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列判断错误的是（　　）
    A、命题“?x∈R，2x＞0”的否定是“?x0∈R，2x0≤0”
    B、命题“若xy=0，则x=0”的否命题为“若xy≠0，则x≠0”
    C、函数y=2x-3+1的图象恒过定点A（3，2）
    D、“sinα=
    1
    2
    ”是“α=
    π
    6
    ”的充分不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=x2-mx+m-1．
    （1）若函数y=lgf（x）在[2，4]上有意义，求实数m的取值范围；
    （2）若函数y=|f（x）|在[-1，0]上单调递减，求实数m的取值范围；
    （3）若对于区间[2，
    5
    2
    ]    内任意两个相异实数x1，x2，总有|f（x1）-f（x2）|≤|x1-x2|成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，动点P（x，y）到F（0，1）的距离比到直线y=-2的距离小1．
    （Ⅰ）求动点P的轨迹W的方程；
    （Ⅱ）过点E（0，-4）的直线与轨迹W交于两点A，B，点D是点E关于x轴的对称点，点A关于y轴的对称点为A1，证明A1，D，B三点共线．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f（x）=ax2+2bx+c，若5a+4b+c=0，f（-1）•f（1）＜0，数列{an}的前n项和Sn=f（n）．
    （1）求证：方程f（x）=0必有两个不等实根x1、x2，且
    4
    3
    ＜x1+x2＜4；
    （2）若c=0，an＞0，且互不相等正整数p，q，n，使得p+q=2n，求证：SpSq＜Sn2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

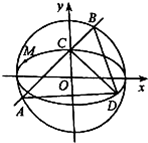    已知椭圆C1：
    x2
    a2
    +
    y2
    b2
    =1(a＞b＞0)    的离心率为
    		3
    2
    ，且经过点M(-
    		3
    ，
    1
    2
    )，圆C2    的直径C1的长轴．如图，C是椭圆短轴端点，动直线AB过点C且与圆C2交于A，B两点，CD垂直于AB交椭圆于点D．
    （Ⅰ）求椭圆C1的方程；
    （Ⅱ）求△ABD面积的最大值，并求此时直线AB的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

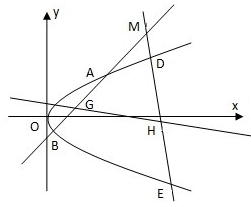    已知抛物线C：y2=2px（p＞0），M点的坐标为（12，8），N点在抛物线C上，且满足
    ON
    =
    3
    4
    OM
    ，O为坐标原点．
    （Ⅰ）求抛物线C的方程；
    （Ⅱ）过点M作倾斜角互补的两条直线l1，l2，l1与抛物线C交于不同两点A，B，l2与抛物线C交于不同两点D，E，弦AB，DE的中点分别为G，H．求当直线l1的倾斜角在[
    π
    6
    ，
    π
    4
    ]时，直线GH被抛物线截得的弦长的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

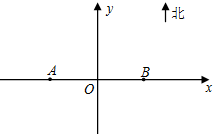    为了监测某海域的船舶航行情况，在该海域设立了如图所示东西走向，相距20海里的A，B两个观测站，观测范围是到A，B两观测站距离之和不超过40海里的区域．
    （Ⅰ）以AB所在直线为x轴，线段AB的垂直平分线为y轴建立平面直角坐标系，求观测区域边界曲线的方程；
    （Ⅱ）某日上午7时，观测站B发现在其正东10海里的C处，有一艘轮船正以每小时8海里的速度向北偏西45°方向航行，问该轮船大约在什么时间离开观测区域？（参考数据：
    		2
    ≈1.4，
    		3
    ≈1.7    ．）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于平面直角坐标系内任意两点A（x1，y1），B（x2，y2），定义它们之间的一种“折线距离”：d（A，B）=|x2-x1|+|y2-y1|．则下列命题正确的是
     
    ．（写出所有正确命题的序号）
    ①若A（-1，3），B（1，0），则d（A，B）=5；
    ②若点C在线段AB上，则d（A，C）+d（C，B）=d（A，B）；
    ③在△ABC中，一定有d（A，C）+d（C，B）＞d（A，B）；
    ④若A为定点，B为动点，且满足d（A，B）=1，则B点的轨迹是一个圆；
    ⑤若A为坐标原点，B在直线2x+y-2
    		5
    =0上，则d（A，B）最小值为
    		5
    ．

    查看答案和解析>>

    同步练习册答案