
分析 然后利用导数研究函数f(x)在区间(1,ea)上的最小值,最后讨论最小值的符号,从而确定函数f(x)的零点情况.
解答 解:f(x)=x2-alnx,(a>0,x>0),
f′(x)=2x-$\frac{a}{x}$=$\frac{{2x}^{2}-a}{x}$=$\frac{2(x-\frac{\sqrt{2a}}{2})(x+\frac{\sqrt{2a}}{2})}{x}$,
因为当0<x<$\frac{\sqrt{2a}}{2}$时,fˊ(x)<0,当x>$\frac{\sqrt{2a}}{2}$时,fˊ(x)>0.
又$\frac{a}{2}$<a<ea<e2a(a≥0,a<2a)⇒$\frac{\sqrt{2a}}{2}$<ea,
所以f(x)在(0,$\frac{\sqrt{2a}}{2}$]上是减函数,在[$\frac{\sqrt{2a}}{2}$,+∞)是增函数.
所以f(x)min=f($\frac{\sqrt{2a}}{2}$)=$\frac{a}{2}$(1-ln$\frac{a}{2}$),
若函数f(x)在区间(1,ea)上有两个零点
则$\frac{a}{2}$(1-ln$\frac{a}{2}$)<0,即a>2e时,ea>$\frac{\sqrt{2a}}{2}$>$\sqrt{e}$,
由于f(1)=1>0,f($\frac{\sqrt{2a}}{2}$)=$\frac{a}{2}$(1-ln$\frac{a}{2}$)<0.
f(ea)=e2a-a lnea=e2a-a2=(ea-a)(ea+a)>0,
所以,函数f(x)在(1,ea)上有两个零点,
综上所述,当a>2e时,函数f(x)有两个零点,
故答案为:(2e,+∞).
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数在闭区间上的最值,同时考查了分类讨论的数学思想和计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
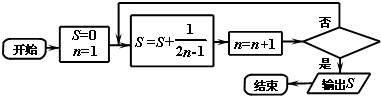
| A. | n>10? | B. | n<11? | C. | n>9? | D. | n>11? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,6] | B. | [6,7] | C. | [$\frac{27}{8}$,7] | D. | [$\frac{27}{8}$,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 0 | D. | 2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
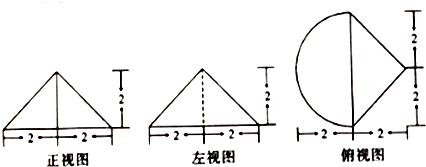
| A. | 4π+8 | B. | $4π+\frac{8}{3}$ | C. | $\frac{4π}{3}+8$ | D. | $\frac{4π+8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com