
已知函数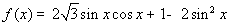 ,x?R.
,x?R.
(1)求函数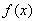 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数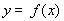 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的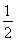 ,把所得到的图象再向左平移
,把所得到的图象再向左平移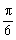 单位,得到函数
单位,得到函数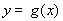 的图象,求函数
的图象,求函数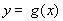 在区间
在区间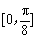 上的最小值.
上的最小值.
(1)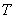 =
=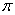 ,递增区间为
,递增区间为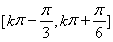 ;(2)
;(2)
【解析】
试题分析:(Ⅰ)先用正弦、余弦二倍角公式将角统一,再用化一公式,将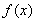 整理成
整理成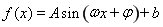 的形式。根据公式
的形式。根据公式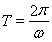 求周期,将角
求周期,将角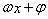 视为整体,代入正弦的单调增区间,即可求得
视为整体,代入正弦的单调增区间,即可求得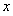 的范围,即
的范围,即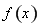 的单调递增区间。(Ⅱ)由(Ⅰ)知
的单调递增区间。(Ⅱ)由(Ⅰ)知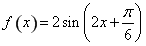 ,函数
,函数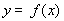 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的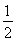 得到
得到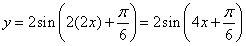 的图像,再向左平移
的图像,再向左平移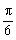 单位得到
单位得到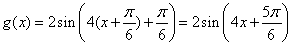 的图像。根据
的图像。根据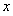 的范围,求整体角
的范围,求整体角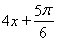 的范围,再根据正弦函数图像求
的范围,再根据正弦函数图像求 的范围,即可求得函数
的范围,即可求得函数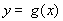 在区间
在区间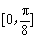 上的最小值。
上的最小值。
试题解析:【解析】
(1)因为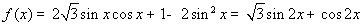
=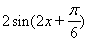 4分
4分
函数f(x)的最小正周期为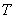 =
=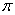 . 6分
. 6分
由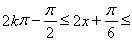
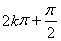 ,
,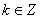 ,
,
得f(x)的单调递增区间为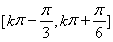 ,
, 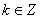 . 8分
. 8分
(2)根据条件得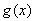 =
=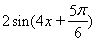 ,当
,当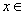
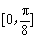 时,
时,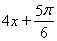
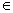
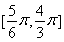 ,
,
所以当x=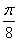 时,
时, . 12分
. 12分
考点:1正弦、余弦二倍角公式、化一公式;2三角函数伸缩平移变换;3三角函数的单调区间及最值;4三角函数图像。


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:选择题
随机变量ξ的分布列如下:
ξ | -1 | 0 | 1 |
P | a | b | c |
其中a,b,c成等差数列,若E(ξ)= ,则D(ξ)的值是( )
,则D(ξ)的值是( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
离散型随机变量X的概率分布规律为P(X=n)=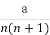 (n=1,2,3,4),其中a是常数,则P(
(n=1,2,3,4),其中a是常数,则P( <X<
<X< )的值为( )
)的值为( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数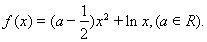
(Ⅰ)当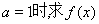 在区间
在区间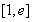 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间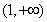 上,函数
上,函数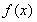 的图象恒在直线
的图象恒在直线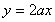 下方,求
下方,求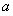 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
设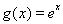 ,
,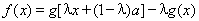 ,其中
,其中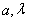 是常数,且
是常数,且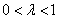 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意正数 ,存在正数
,存在正数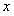 ,使不等式
,使不等式 成立;
成立;
(3)设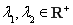 ,且
,且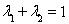 ,证明:对任意正数
,证明:对任意正数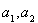 都有:
都有: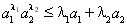 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com