
设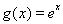 ,
,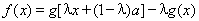 ,其中
,其中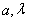 是常数,且
是常数,且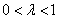 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意正数 ,存在正数
,存在正数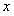 ,使不等式
,使不等式 成立;
成立;
(3)设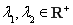 ,且
,且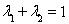 ,证明:对任意正数
,证明:对任意正数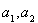 都有:
都有: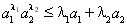 .
.
(1)当 时,
时, 取极大值,但
取极大值,但 没有极小值(2)见解析(3)见解析
没有极小值(2)见解析(3)见解析
【解析】(1)∵ , -----------------1分
, -----------------1分
由 得,
得,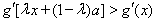 ,
,
∴ ,即
,即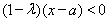 ,解得
,解得 ,-----------------3分
,-----------------3分
故当 时,
时, ;当
;当 时,
时, ;
;
∴当 时,
时, 取极大值,但
取极大值,但 没有极小值.-----------------4分
没有极小值.-----------------4分
(2)∵ ,
,
又当 时,令
时,令 ,则
,则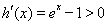 ,
,
故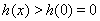 ,
,
因此原不等式化为 ,即
,即 , -----------------6分
, -----------------6分
令 ,则
,则 ,
,
由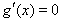 得:
得: ,解得
,解得 ,
,
当 时,
时, ;当
;当 时,
时, .
.
故当 时,
时, 取最小值
取最小值 ,-----------------8分
,-----------------8分
令 ,则
,则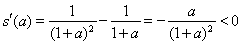 .
.
故 ,即
,即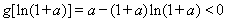 .
.
因此,存在正数 ,使原不等式成立.-----------------10分
,使原不等式成立.-----------------10分
(3)对任意正数 ,存在实数
,存在实数 使
使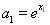 ,
,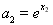 ,
,
则 ,
, ,
,
原不等式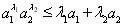
 ,
,
 -----------------14分
-----------------14分
由(1) 恒成立,
恒成立,
故 ,
,
取 ,
,
即得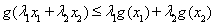 ,
,
即 ,故所证不等式成立. -----------------14分
,故所证不等式成立. -----------------14分


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:填空题
若随机变量ξ的分布列为:P(ξ=m)= ,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 .
,P(ξ=n)=a.若E(ξ)=2,则D(ξ)的最小值等于 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:填空题
随机变量η的分布列如下:
η | 1 | 2 | 3 | 4 | 5 | 6 |
P | 0.2 | x | 0.35 | 0.1 | 0.15 | 0.2 |
则①x= ;②P(η>3)= ;
③P(1<η≤4)= .
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数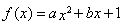 在
在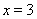 处的切线方程为
处的切线方程为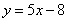 .
.
(1)求函数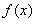 的解析式;
的解析式;
(2)若关于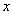 的方程
的方程 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数 的值;
的值;
(3)数列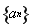 满足
满足 ,
,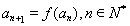 ,求
,求 的整数部分.
的整数部分.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数 ,
,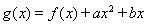 ,函数
,函数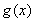 的图象在点
的图象在点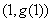 处的切线平行于
处的切线平行于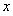 轴.
轴.
(1)确定 与
与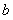 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意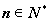 ,都有
,都有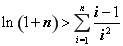 成立。
成立。
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:解答题
已知函数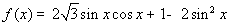 ,x?R.
,x?R.
(1)求函数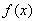 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数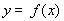 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的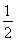 ,把所得到的图象再向左平移
,把所得到的图象再向左平移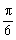 单位,得到函数
单位,得到函数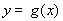 的图象,求函数
的图象,求函数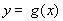 在区间
在区间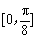 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:填空题
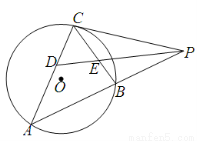
如图,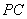 是圆
是圆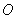 的切线,切点为点
的切线,切点为点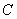 ,直线
,直线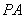 与圆
与圆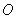 交于
交于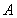 、
、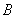 两点,
两点,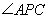 的角平分线交弦
的角平分线交弦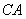 、
、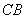 于
于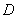 、
、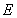 两点,已知
两点,已知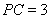 ,
,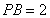 ,则
,则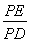 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:解答题
设函数f(x)=sin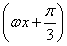 +sin
+sin +
+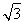 cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为
cos ωx(其中ω>0),且函数f(x)的图象的两条相邻的对称轴间的距离为 .
.
(1)求ω的值;
(2)将函数y=f(x)的图象上各点的横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间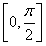 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com