
已知函数 ,
,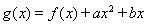 ,函数
,函数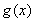 的图象在点
的图象在点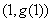 处的切线平行于
处的切线平行于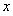 轴.
轴.
(1)确定 与
与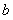 的关系;
的关系;
(2)试讨论函数 的单调性;
的单调性;
(3)证明:对任意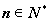 ,都有
,都有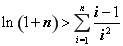 成立。
成立。
(1)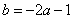 (2)当
(2)当 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在 单调递减;当
单调递减;当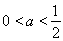 时,函数
时,函数 在
在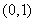 单调递增,在
单调递增,在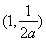 单调递减;在
单调递减;在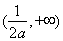 上单调递增;当
上单调递增;当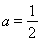 时,函数
时,函数 在
在 上单调递增,当
上单调递增,当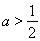 时,函数
时,函数 在
在 上单调递增,在
上单调递增,在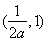 单调递减;在
单调递减;在 上单调递增(3)见解析
上单调递增(3)见解析
【解析】(1)依题意得 ,则
,则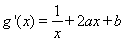
由函数 的图象在点
的图象在点 处的切线平行于
处的切线平行于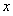 轴得:
轴得: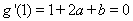
 ∴
∴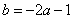 -------------------------------------3分
-------------------------------------3分
(2)由(1)得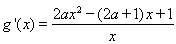
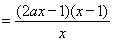 ----------4分
----------4分
∵函数 的定义域为
的定义域为
∴当 时,
时,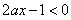 在
在 上恒成立,
上恒成立,
由 得
得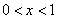 ,由
,由 得
得 ,
,
即函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在 单调递减;----------------5分
单调递减;----------------5分
当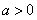 时,令
时,令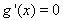 得
得 或
或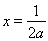 ,
,
若 ,即
,即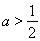 时,由
时,由 得
得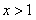 或
或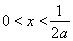 ,由
,由 得
得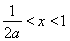 ,
,
即函数 在
在 ,
, 上单调递增,在
上单调递增,在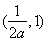 单调递减;---------6分
单调递减;---------6分
若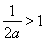 ,即
,即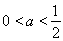 时,由
时,由 得
得 或
或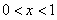 ,由
,由 得
得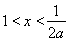 ,
,
即函数 在
在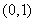 ,
,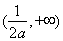 上单调递增,在
上单调递增,在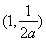 单调递减;------------7分
单调递减;------------7分
若 ,即
,即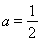 时,在
时,在 上恒有
上恒有 ,
,
即函数 在
在 上单调递增, -----------------8分
上单调递增, -----------------8分
综上得:当 时,函数
时,函数 在(0,1)上单调递增,在
在(0,1)上单调递增,在 单调递减;
单调递减;
当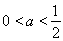 时,函数
时,函数 在
在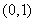 单调递增,在
单调递增,在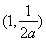 单调递减;在
单调递减;在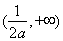 上单调递增;
上单调递增;
当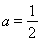 时,函数
时,函数 在
在 上单调递增,
上单调递增,
当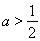 时,函数
时,函数 在
在 上单调递增,在
上单调递增,在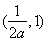 单调递减;在
单调递减;在 上单调递增.
上单调递增.
(3)证法一:由(2)知当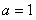 时,函数
时,函数 在
在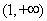 单调递增,
单调递增, ,即
,即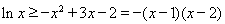 ,------------11分
,------------11分
令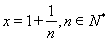 ,则
,则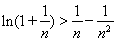 ,-------------------------------------12分
,-------------------------------------12分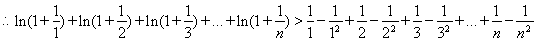
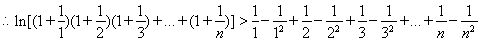
即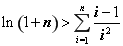 --------14分
--------14分
证法二:构造数列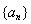 ,使其前
,使其前 项和
项和 ,
,
则当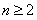 时,
时,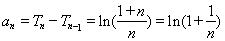 ,-------11分
,-------11分
显然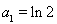 也满足该式,
也满足该式,
故只需证 -------------------12分
-------------------12分
令 ,即证
,即证 ,记
,记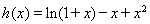 ,
,
则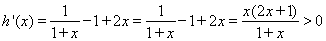 ,
,
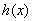 在
在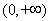 上单调递增,故
上单调递增,故 ,
,
∴ 成立,
成立,
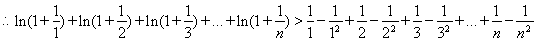
即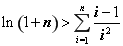 . -14分
. -14分


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨.现由天气预报得知,某地在未来5天的指定时间的降雨概率是:前3天均为50%,后2天均为80%,5天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.
(1)求至少有1天需要人工降雨的概率.
(2)求不需要人工降雨的天数x的分布列和期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十七选修4-4第一节练习卷(解析版) 题型:解答题
求经过极点O(0,0),A(6, ),B(6
),B(6 ,
, )三点的圆的极坐标方程.
)三点的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数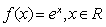 的图象与
的图象与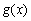 的图象关于直线
的图象关于直线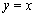 对称。
对称。
(Ⅰ)若直线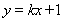 与
与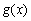 的图像相切, 求实数
的图像相切, 求实数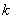 的值;
的值;
(Ⅱ)判断曲线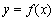 与曲线
与曲线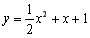 公共点的个数.
公共点的个数.
(Ⅲ)设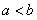 ,比较
,比较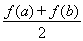 与
与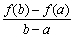 的大小, 并说明理由.
的大小, 并说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数 ,
, 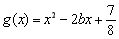 .
.
(Ⅰ)当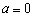 时,求曲线
时,求曲线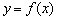 在点
在点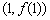 处的切线方程;
处的切线方程;
(Ⅱ)当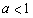 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)当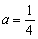 时,函数
时,函数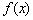 在
在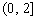 上的最大值为
上的最大值为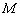 ,若存在
,若存在 ,使得
,使得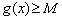 成立,求实数b的取值范围.
成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
设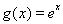 ,
,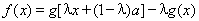 ,其中
,其中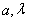 是常数,且
是常数,且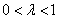 .
.
(1)求函数 的极值;
的极值;
(2)证明:对任意正数 ,存在正数
,存在正数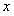 ,使不等式
,使不等式 成立;
成立;
(3)设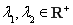 ,且
,且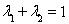 ,证明:对任意正数
,证明:对任意正数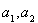 都有:
都有: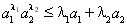 .
.
查看答案和解析>>
科目:高中数学 来源:2014年广东省广州市毕业班综合测试一理科数学试卷(解析版) 题型:解答题
已知双曲线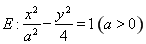 的中心为原点
的中心为原点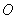 ,左、右焦点分别为
,左、右焦点分别为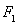 、
、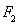 ,离心率为
,离心率为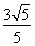 ,点
,点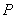 是直线
是直线 上任意一点,点
上任意一点,点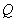 在双曲线
在双曲线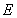 上,且满足
上,且满足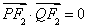 .
.
(1)求实数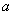 的值;
的值;
(2)证明:直线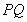 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为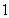 ,过点
,过点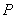 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、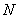 ,在线段
,在线段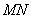 上去异于点
上去异于点 、
、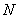 的点
的点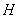 ,满足
,满足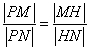 ,证明点
,证明点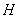 恒在一条定直线上.
恒在一条定直线上.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)仿真模拟卷2练习卷(解析版) 题型:解答题
过椭圆Γ: =1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为 .
.
(1)求椭圆Γ的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点P,Q,且 ⊥
⊥ ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com