
(本小题12分)某产品原来的成本为1000元/件,售价为1200元/件,年销售量为1万件。由于市场饱和顾客要求提高,公司计划投入资金进行产品升级。据市场调查,若投入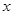 万元,每件产品的成本将降低
万元,每件产品的成本将降低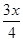 元,在售价不变的情况下,年销售量将减少
元,在售价不变的情况下,年销售量将减少 万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为
万件,按上述方式进行产品升级和销售,扣除产品升级资金后的纯利润记为 (单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(单位:万元).(纯利润=每件的利润×年销售量-投入的成本)
(Ⅰ)求 的函数解析式;
的函数解析式;
(Ⅱ)求 的最大值,以及
的最大值,以及 取得最大值时
取得最大值时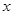 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题共12分)水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=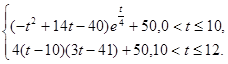
(Ⅰ)该水库的蓄水量小于50的时期称为枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(文科题)(本小题12分)
要建造一个无盖长方体水池,底面一边长固定为8m,最大装水量为72m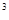 ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2 元/
元/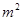 、
、 元/
元/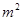 ,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
,怎样设计水池底的另一边长和水池的高,才能使水池的总造价最低?最低造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
设平面直角坐标系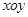 中,设二次函数
中,设二次函数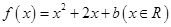 的图象与两坐标轴有三个交点,经过这三个交点的圆记为
的图象与两坐标轴有三个交点,经过这三个交点的圆记为 .求:
.求:
(Ⅰ)求实数 的取值范围;
的取值范围;
(Ⅱ)求圆 的方程;
的方程;
(Ⅲ)问圆 是否经过某定点(其坐标与b 无关)?请证明你的结论.
是否经过某定点(其坐标与b 无关)?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)某公司生产的新产品的成本是2元/件,售价是3元/件,
年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是 (万元)时,产品的销售量将是原销售量的
(万元)时,产品的销售量将是原销售量的 倍,且
倍,且 是
是 的二次函数,它们的关系如下表:
的二次函数,它们的关系如下表:
 | ··· | 1 | 2 | ··· | 5 | ··· |
 | ··· | 1.5 | 1.8 | ··· | 1.5 | ··· |
 与
与 的函数关系式;
的函数关系式; 成本费
成本费 广告费,试写出年利润S(万元)与广告费
广告费,试写出年利润S(万元)与广告费 (万元)的函数关系式;并求出当广告费
(万元)的函数关系式;并求出当广告费 为多少万元时,年利润S最大.
为多少万元时,年利润S最大.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)病人按规定的剂量服用某药物,测得服药后,每毫升血液中含药量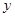 (毫克)与时间
(毫克)与时间 (小时)满足:前1小时内成正比例递增,1小时后按指数型函数
(小时)满足:前1小时内成正比例递增,1小时后按指数型函数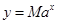 (
(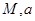 为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
为常数)衰减.如图是病人按规定的剂量服用该药物后,每毫升血液中药物含量随时间变化的曲线.
(1)求函数 的解析式;
的解析式;
(2)已知每毫升血液中含药量不低于0.5毫克时有治疗效果,低于0.5毫克时无治疗效果.求病人一次服药后的有效治疗时间为多少小时?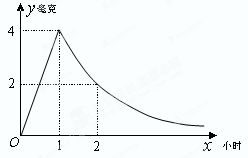
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知f(x)=logax,g(x)=2loga(2x+t-2)(a>0,a≠1,t∈R).
(1)当t=4,x∈[1,2],且F(x)=g(x)-f(x)有最小值2时,求a的值;
(2)当0<a<1,x∈[1,2]时,有f(x)≥g(x)恒成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com