若函数f(x)=x2+ax+b有两个不同的零点x1,x2,且1<x1<x2<3,那么在f(1),f(3)两个函数值中( )
A.只有一个小于1
B.至少有一个小于1
C.都小于1
D.可能都大于1
【答案】
分析:由题意可得f(x)=(x-x
1)(x-x
2),利用基本不等式可得故f(1)•f(3)<1,由此可得两个函数值f(1)、f(3)
中至少有一个小于1.
解答:解:由题意可得函数f(x)=(x-x
1)(x-x
2),
∴f(1)=(1-x
1)(1-x
2)=(x
1-1)(x
2-1),f(3)=(3-x
1)(3-x
2),
∴f(1)•f(3)=(x
1-1)(x
2-1)(3-x
1)(3-x
2)=(x
1-1)(3-x
1)(x
2-1)(3-x
2)
<
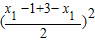
•
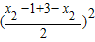
=1×1=1,
即 f(1)•f(3)<1.
故f(1),f(3)两个函数值中至少有一个小于1,
故选:B.
点评:本题主要考查一元二次方程根的分布与系数的关系,本题解题的关键是把函数表示成两点式,利用基本不等式求出函数的最值,属于中档题.

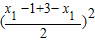 •
•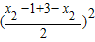 =1×1=1,
=1×1=1,

 阅读快车系列答案
阅读快车系列答案