
 (x>1),
(x>1),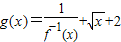 ,求g(x)的最小值;
,求g(x)的最小值; 对于一切
对于一切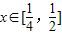 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)已知af(x)+bf(![]() )=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
)=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
(3)f(x)是R上的奇函数,且x∈(-∞,0)时,f(x)=x2+2x,求f(x);
(4)某工厂生产一种机器的固定成本为5 000元,且每生产100部,需要增加投入2 500元,对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入的函数为H(x)=500x-![]() x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
x2,其中x是产品售出的数量,且0≤x≤500.若x为年产量,y表示利润,求y=f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)证明:f(x)在(-1,1)上为奇函数;
(2)求f(xn)的表达式;
(3)是否存在自然数m,使得对于任意n∈N*,![]() 恒成立?若存在,求出m的最小值.
恒成立?若存在,求出m的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com