
【题目】已知函数f(x)=x2﹣alnx,a>0.
(1)若f(x)在x=1处取得极值,求实数a的值;
(2)求f(x)在区间[2,+∞)上的最小值;
(3)在(1)的条件下,若g(x)=x2﹣f(x),求证:当1<x<e2,恒有x![]() .
.
【答案】(1)2(2)当0<a≤8时,最小值为4﹣2ln2;当a>8时,最小值为![]() (3)证明见解析
(3)证明见解析
【解析】
(1)利用![]() 列方程,由此求得
列方程,由此求得![]() 的可能取值,验证后求得
的可能取值,验证后求得![]() 的值.
的值.
(2)求得![]() 的定义域和导函数,根据
的定义域和导函数,根据![]() 两种情况进行分类讨论,结合函数
两种情况进行分类讨论,结合函数![]() 的单调区间,求得
的单调区间,求得![]() 在区间
在区间![]() 上的最小值.
上的最小值.
(3)求得![]() ,判断出
,判断出![]() ,将要证明的不等式转化为
,将要证明的不等式转化为![]() ,构造函数
,构造函数![]() ,利用导数证得
,利用导数证得![]() ,由此证得不等式成立.
,由此证得不等式成立.
(1)由f(x)=x2﹣alnx知,函数的定义域为(0,+∞),![]() ,∵函数f(x)在x=1处取得极值,∴f′(1)=0,即2﹣a=0,解得a=2,经检验,满足题意,故a=2;
,∵函数f(x)在x=1处取得极值,∴f′(1)=0,即2﹣a=0,解得a=2,经检验,满足题意,故a=2;
(2)由(1)得![]() ,定义域为(0,+∞),当0<a≤8时,由f′(x)=0得
,定义域为(0,+∞),当0<a≤8时,由f′(x)=0得![]() ,且
,且![]() ,当
,当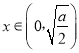 时,f′(x)<0,f(x)单调递减,当
时,f′(x)<0,f(x)单调递减,当 时,f′(x)>0,f(x)单调递增,∴f(x)在区间[2,+∞)上单调递增,最小值为f(2)=4﹣2ln2,当a>8时,
时,f′(x)>0,f(x)单调递增,∴f(x)在区间[2,+∞)上单调递增,最小值为f(2)=4﹣2ln2,当a>8时,![]() ,当
,当 时,f′(x)<0,f(x)单调递减,当
时,f′(x)<0,f(x)单调递减,当 时,f′(x)>0,f(x)单调递增,∴函数f(x)在
时,f′(x)>0,f(x)单调递增,∴函数f(x)在![]() 处取得最小值
处取得最小值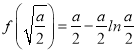 ,综上,当0<a≤8时,f(x)在区间[2,+∞)上的最小值为4﹣2ln2;当a>8时,f(x)在区间[2,+∞)上的最小值为
,综上,当0<a≤8时,f(x)在区间[2,+∞)上的最小值为4﹣2ln2;当a>8时,f(x)在区间[2,+∞)上的最小值为![]() ;
;
(3)由g(x)=x2﹣f(x)得g(x)=2lnx,当1<x<e2时,0<lnx<2,0<g(x)<4,欲证![]() ,只需证x[4﹣g(x)]<4+g(x),即证
,只需证x[4﹣g(x)]<4+g(x),即证![]() ,即
,即![]() ,设
,设![]() ,则
,则![]() ,当1<x<e2时,φ′(x)>0,所以φ(x)在区间(1,e2)上单调递增,∴φ(x)>φ(1)=0,即
,当1<x<e2时,φ′(x)>0,所以φ(x)在区间(1,e2)上单调递增,∴φ(x)>φ(1)=0,即![]() ,∴
,∴![]() ,由此得证.
,由此得证.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面 ABCD为矩形,侧面为正三角形,且平面
中,底面 ABCD为矩形,侧面为正三角形,且平面![]() 平面
平面 ![]() E 为 PD 中点,AD=2.
E 为 PD 中点,AD=2.
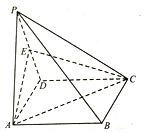
(1)证明平面AEC丄平面PCD;
(2)若二面角![]() 的平面角
的平面角![]() 满足
满足![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域和值域均为![]() (常数
(常数![]() )的函数
)的函数![]() 和y=g(x)的图像如图所示,给出下列四个命题:
和y=g(x)的图像如图所示,给出下列四个命题:
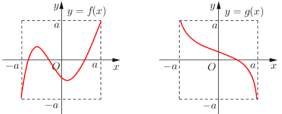
(1)方程![]() 有且仅有三个解;
有且仅有三个解;
(2)方程![]() 有且仅有三个解;
有且仅有三个解;
(3)方程![]() 有且仅有九个解;
有且仅有九个解;
(4)方程![]() 有且仅有一个解;
有且仅有一个解;
那么,其中正确命题的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等腰梯形MNCD中,MD∥NC,MN=![]() MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC
MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC

(1)求证:DE⊥平面ABCE;
(2)求点A到平面DBE的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】砂糖橘是柑橘类的名优品种,因其味甜如砂糖故名.某果农选取一片山地种植砂糖橘,收获时,该果农随机选取果树20株作为样本测量它们每一株的果实产量(单位:kg),获得的所有数据按照区间(40,45],(45,50],(50,55],(55,60]进行分组,得到频率分布直方图如图所示.已知样本中产量在区间(45,50]上的果树株数是产量在区间(50,60]上的果树株数的![]() 倍.
倍.

(1)求a,b的值;
(2)从样本中产量在区间(50,60]上的果树里随机抽取两株,求产量在区间(55,60]上的果树至少有一株被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px经过点
=2px经过点![]() (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(1)根据已知数据,把表格数据填写完整;
(2)若在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,求从这5人中随机抽取3人至多有1人是教师的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有2位男生,3位女生去参加一个联欢活动,该活动有甲、乙两个项目可供参加者选择.
(Ⅰ)为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个项目联欢,掷出点数为1或2的人去参加甲项目联欢,掷出点数大于2的人去参加乙项目联欢.求这5人中恰好有3人去参加甲项目联欢的概率;
(Ⅱ)若从这5人中随机选派3人去参加甲项目联欢,设![]() 表示这3个人中女生的人数,求随机变量
表示这3个人中女生的人数,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com