练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某企业准备投资 万元兴办一所中学，对当地教育市场进行调查后，得到了如下的数据表格（以班级为单位）：

    初中

    26

    4

    高中

    54

    6

    第一年因生源和环境等因素，全校总班级至少 个，至多 个，若每开设一个初、高中班，可分别获得年利润 万元、 万元，则第一年利润最大为

    A. 万元 B. 万元 C. 万元 D. 万元

    【答案】A

    【解析】分析：设开设初中班个，高中班个，利润为，则，根据题意得到约束条件，然后根据线性规划求解．

    详解：设开设初中班个，高中班个，利润为，则．

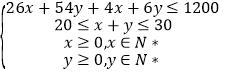    由题意得满足的条件为，即．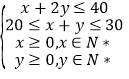

    画出不等式组表示的可行域，如图阴影部分所示．

    [Failed to download image : http://192.168.0.10:8086/QBM/2018/5/30/1956367377481728/1957962440146944/EXPLANATION/01dbe2cd0e5c474db8d28df00165e8d6.png]

    由，得．平移直线（图中的虚线），结合图形可得，当直线经过可行域内的点M时，直线在y轴上的截距最大，此时z取得最大值．

    由解得．故点M的坐标为（20,10）．

    ∴(万元)，

    即第一年利润最大为70万元．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知在四棱锥C﹣ABDE中，DB⊥平面ABC，AE∥DB，△ABC是边长为2的等边三角形，AE=1，M为AB的中点．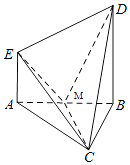
    （1）求证：CM⊥EM；
    （2）若直线DM与平面ABC所成角的正切值为2，求二面角B﹣CD﹣E的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在平面直角坐标系 中的一个椭圆，它的中心在原点，左焦点为 ,右顶点为 ,设点 ．
    （1）求该椭圆的标准方程；
    （2）若 是椭圆上的动点，求线段 中点 的轨迹方程；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其函数图象的相邻两条对称轴之间的距离为.

    （1）求函数的解析式及对称中心；

    （2）将函数的图象向左平移个单位长度，再向上平移个单位长度得到函数的图象，若关于的方程在区间上有两个不相等的实根，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为实数，设函数，设

    ．

    （1）求的取值范围，并把表示为的函数；

    （2）若恒成立，求实数的取值范围；

    （3）若存在使得成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

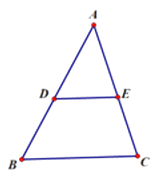
    【题目】如图，已知点 分别是Δ 的边 的中点，连接 .现将 沿 折叠至Δ 的位置,连接 .记平面 与平面 的交线为 ，二面角 大小为 .

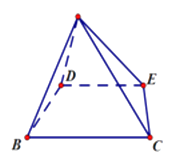
    （1）证明：
    （2）证明：
    （3）求平面 与平面 所成锐二面角大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设 为等差数列 的前 项和，其中 ，且 ．

    （1）求常数 的值，并写出 的通项公式；

    （2）记 ，数列 的前 项和为 ，若对任意的 ，都有 ，求常数 的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知以点 为圆心的圆与直线 相切，过点 的直线 与圆 相交于 两点， 是 的中点， .
    （1）求圆 的标准方程；
    （2）求直线 的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在等腰直角中，，，点在线段上.

    (Ⅰ) 若，求的长；

    （Ⅱ）若点在线段上，且，问：当取何值时，的面积最小？并求出面积的最小值.

    查看答案和解析>>

    同步练习册答案