
【题目】对于某种类型的口服药,口服![]() 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度![]() (单位)与时间
(单位)与时间![]() 小时的关系为
小时的关系为![]() ,其中
,其中![]() ,
,![]() 为常数,对于某一种药物
为常数,对于某一种药物![]() ,
,![]() ,
,![]() .
.
(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药![]() 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)
【答案】![]() 15:00
15:00
【解析】
根据题意,代入参数后可得解析式,结合二次函数性质即可求得最大值及取最大值时自变量的值;由所给数据,满足病人血液中药物浓度保持在0.5个单位以上的条件,即可得解.
药物浓度![]() (单位)与时间
(单位)与时间![]() 小时的关系为
小时的关系为![]() ,对于某一种药物
,对于某一种药物![]() ,
,![]() ,
,![]() .
.
代入可得![]()
![]()

 ,
,
所以当![]() ,即
,即![]() 时取得最大值;
时取得最大值;
由表中数据可知,病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,则第二次服药时间在11:00;第一次服药后7个小时后药物残留为0.1163,第二次服药后4小时的药物残留为0.4680,而![]() .
.
第一次服药后8小时的药物残留为0.072,第二次服药后4小时的药物残留为0.3010,而![]() ;
;
综上可知,若使得病人血液中药物浓度保持在0.5个单位以上,则第三次服药时间为第一次服药后的7小时,即为15:00.
故答案为:![]() ;15:00.
;15:00.


科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 平面
平面![]() ,且
,且![]() .
.
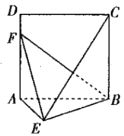
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二而角
,使二而角![]() 等于45°?若存在,请找出点
等于45°?若存在,请找出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形ABCD为平行四边形,且
中,四边形ABCD为平行四边形,且![]() ,
,![]() ,
,![]() 平面PAC.
平面PAC.

(1)求证:![]() 平面
平面![]() ;
;
(2)若异面直线PC与AD所成的角为30°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为![]() ,
,

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,问在
两点,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?证明你的结论.
为定值?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是一个单调递增的等比数列,
是一个单调递增的等比数列,![]() 是一个等差数列,
是一个等差数列,![]() 是
是![]() 的前
的前![]() 项和,其中
项和,其中![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() 既成等比数列,又成等差数列.
既成等比数列,又成等差数列.
(i)求![]() 的通项公式;
的通项公式;
(ii)对于数列![]() ,若
,若![]() 且
且![]() ,或
,或![]() 且
且![]() ,则
,则![]() 为数列
为数列![]() 的转折点,求
的转折点,求![]() 的转折点个数.
的转折点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
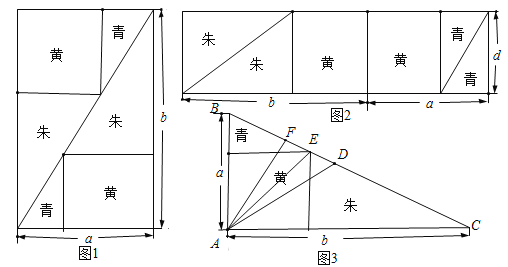
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得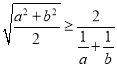 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com