
【题目】已知![]() 是一个单调递增的等比数列,
是一个单调递增的等比数列,![]() 是一个等差数列,
是一个等差数列,![]() 是
是![]() 的前
的前![]() 项和,其中
项和,其中![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() 既成等比数列,又成等差数列.
既成等比数列,又成等差数列.
(i)求![]() 的通项公式;
的通项公式;
(ii)对于数列![]() ,若
,若![]() 且
且![]() ,或
,或![]() 且
且![]() ,则
,则![]() 为数列
为数列![]() 的转折点,求
的转折点,求![]() 的转折点个数.
的转折点个数.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,
,![]() ,求实数
,求实数![]() 的最小值;
的最小值;
(Ⅲ)当![]() 时,给出一个新数列
时,给出一个新数列![]() ,其中
,其中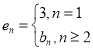 ,设这个新数列的前
,设这个新数列的前![]() 项和为
项和为![]() ,若
,若![]() 可以写成
可以写成![]() (
(![]() ,
,![]() 且
且![]() ,
,![]() )的形式,则称
)的形式,则称![]() 为“指数型和”.问
为“指数型和”.问![]() 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于某种类型的口服药,口服![]() 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度![]() (单位)与时间
(单位)与时间![]() 小时的关系为
小时的关系为![]() ,其中
,其中![]() ,
,![]() 为常数,对于某一种药物
为常数,对于某一种药物![]() ,
,![]() ,
,![]() .
.
(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药![]() 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中点(如图1),将
是EA的中点(如图1),将![]() 沿CD折起到图2中
沿CD折起到图2中![]() 的位置,得到四棱锥是
的位置,得到四棱锥是![]() .
.
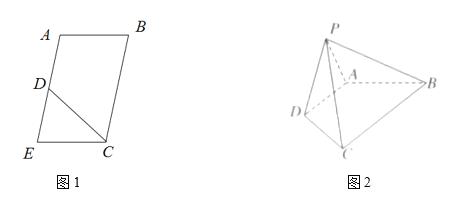
(1)求证:![]() 平面PDA;
平面PDA;
(2)若PD与平面ABCD所成的角为![]() .且
.且![]() 为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为进一步规范校园管理,强化饮食安全,提出了“远离外卖,健康饮食”的口号.当然,也需要学校食堂能提供安全丰富的菜品来满足同学们的需求.在学期末,校学生会为了调研学生对本校食堂A部和B部的用餐满意度,从在A部和B部都用过餐的学生中随机抽取了200人,每人分别对其评分,满分为100分.随后整理评分数据,将分数分成6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到A部分数的频率分布直方图和B部分数的频数分布表.
,得到A部分数的频率分布直方图和B部分数的频数分布表.

分数区间 | 频数 |
| 7 |
| 18 |
| 21 |
| 24 |
| 70 |
| 60 |
定义:学生对食堂的“满意度指数”
分数 |
|
|
|
|
|
|
满意度指数 | 0 | 1 | 2 | 3 | 4 | 5 |
(1)求A部得分的中位数(精确到小数点后一位);
(2)A部为进一步改善经营,从打分在80分以下的前四组中,采用分层抽样的方法抽取8人进行座谈,再从这8人中随机抽取3人参与“端午节包粽子”实践活动,在第3组抽到1人的情况下,第4组抽到2人的概率;
(3)如果根据调研结果评选学生放心餐厅,应该评选A部还是B部(将频率视为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
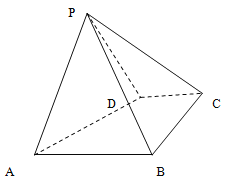
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,且
,且![]() 为常数).
为常数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线的斜率为
处的切线的斜率为![]() (
(![]() 为自然对数的底数),求
为自然对数的底数),求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,且
,且![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 上点
上点![]() 作三条斜率分别为
作三条斜率分别为![]() ,
,![]() ,
,![]() 的直线
的直线![]() ,
,![]() ,
,![]() ,与抛物线分别交于不同于
,与抛物线分别交于不同于![]() 的点
的点![]() .若
.若![]() ,
,![]() ,则以下结论正确的是( )
,则以下结论正确的是( )
A.直线![]() 过定点B.直线
过定点B.直线![]() 斜率一定
斜率一定
C.直线![]() 斜率一定D.直线
斜率一定D.直线![]() 斜率一定
斜率一定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com