Question

11．已知在平面直角坐标系中，$\left\{\begin{array}{l}{x≤2}\\{x+y≥4}\\{x-y≥-2}\end{array}\right.$，表示的平面区域为Ω，O（0，0），A（1，0），若M∈Ω．则$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|}$的取值范围是[-$\frac{\sqrt{10}}{10}$，$\frac{\sqrt{2}}{2}$]．

Answer 1

分析 作出不等式组对应的平面区域，利用平面向量的数量积进行转化，利用数形结合进行求解即可．

解答 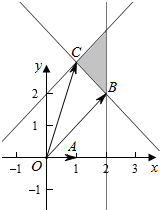解：$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|}$=|$\overrightarrow{OA}$|•$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|•|\overrightarrow{OA}|}$=|$\overrightarrow{OA}$|•cos＜$\overrightarrow{OA}$，$\overrightarrow{OM}$＞，
作出不等式组对应的平面区域如图：
由图象知当M位于B时$\overrightarrow{OA}$，$\overrightarrow{OM}$的夹角最小，
当M位于C时$\overrightarrow{OA}$，$\overrightarrow{OM}$的夹角最大，
由$\left\{\begin{array}{l}{x=2}\\{x+y=4}\end{array}\right.$，即$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$，此时B（2，2），则cos＜$\overrightarrow{OA}$，$\overrightarrow{OM}$＞=$\frac{\sqrt{2}}{2}$，
由$\left\{\begin{array}{l}{x+y=4}\\{x-y=-2}\end{array}\right.$，即$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$，此时C（1，3），则cos＜$\overrightarrow{OA}$，$\overrightarrow{OM}$＞=$\frac{1}{\sqrt{{1}^{2}+{3}^{2}}}$=$\frac{1}{\sqrt{10}}$=$\frac{\sqrt{10}}{10}$，
故-$\frac{\sqrt{10}}{10}$≤cos＜$\overrightarrow{OA}$，$\overrightarrow{OM}$＞≤$\frac{\sqrt{2}}{2}$，
即-$\frac{\sqrt{10}}{10}$≤$\frac{\overrightarrow{OA}•\overrightarrow{OM}}{|\overrightarrow{OM}|}$≤$\frac{\sqrt{2}}{2}$，
故答案为：[-$\frac{\sqrt{10}}{10}$，$\frac{\sqrt{2}}{2}$]

点评 本题主要考查线性规划的应用，利用平面向量的数量积进行转化以及利用数形结合是解决本题的关键．