
【题目】已知二次函数![]() 的对称轴为
的对称轴为![]() ,
,![]() .
.
(1)求函数![]() 的最小值及取得最小值时
的最小值及取得最小值时![]() 的值;
的值;
(2)试确定![]() 的取值范围,使
的取值范围,使![]() 至少有一个实根;
至少有一个实根;
(3)当![]() 时,
时,![]() ,对任意
,对任意![]() 有
有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,此时
,此时![]() ;(2)
;(2)![]() 的取值范围为
的取值范围为![]() ;(3)实数
;(3)实数![]() 的取值范围为
的取值范围为![]() .
.
【解析】
试题分析:(1)利用基本不等式易得![]() ,此时
,此时![]() .(2)
.(2)![]() 至少有一个实根,即
至少有一个实根,即![]() 与
与![]() 的图象在
的图象在![]() 上至少有一个交点,由题意,可得
上至少有一个交点,由题意,可得![]() ,
,![]() ,则需
,则需![]() 即可;(3)由题意,可得
即可;(3)由题意,可得![]() ,对任意
,对任意![]() 有
有![]() 恒成立,即
恒成立,即![]() ,令
,令![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
令![]() ,讨论函数
,讨论函数![]() 的单调性,即可得到实数
的单调性,即可得到实数![]() 的取值范围.
的取值范围.
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时“=”成立,即
时“=”成立,即![]() ,此时
,此时![]() .
.
(2)![]() 的对称轴为
的对称轴为![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
![]() 至少有一个实根,∴
至少有一个实根,∴![]() 至少有一个实根,
至少有一个实根,
即![]() 与
与![]() 的图象在
的图象在![]() 上至少有一个交点,
上至少有一个交点,
![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 的取值范围为
的取值范围为![]() .
.
(3)∵![]() ,∴
,∴![]() ,
,
∴对任意![]() 有
有![]() 恒成立,∴
恒成立,∴![]() ,
,
令![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
令![]() ,设
,设![]() 为
为![]() 上任意两不等实数,且
上任意两不等实数,且![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,∴
,∴![]() .
.
∴实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号.如果两个编号的和为偶数就算甲胜,否则算乙胜.
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)函数![]() 的图象与
的图象与![]() 的图象无公共点,求实数
的图象无公共点,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,请求出整数
的图象的下方?若存在,请求出整数![]() 的最大值;若不存在,请说理由.
的最大值;若不存在,请说理由.
(参考数据:![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为方便市民休闲观光,市政府计划在半径为200米,圆心角为![]() 的扇形广场内(如图所示),沿
的扇形广场内(如图所示),沿![]() 边界修建观光道路,其中
边界修建观光道路,其中![]() 分别在线段
分别在线段![]() 上,且
上,且![]() 两点间距离为定长
两点间距离为定长![]() 米.
米.
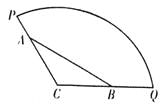
(1)当![]() 时,求观光道
时,求观光道![]() 段的长度;
段的长度;
(2)为提高观光效果,应尽量增加观光道路总长度,试确定图中![]() 两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
两点的位置,使观光道路总长度达到最长?并求出总长度的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次篮球定点投篮训练中,规定每人最多投3次,在![]() 处每投进一球得3分;在
处每投进一球得3分;在![]() 处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在
处每投进一球得2分,如果前两次得分之和超过3分就停止投篮;否则投第3次,某同学在![]() 处的抽中率
处的抽中率![]() ,在
,在![]() 处的抽中率为
处的抽中率为![]() ,该同学选择现在
,该同学选择现在![]() 处投第一球,以后都在
处投第一球,以后都在![]() 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用![]() 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的数学期望
的数学期望![]() ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在![]() 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() , 若
, 若![]() 成等比数列,椭圆
成等比数列,椭圆![]() 上的点到焦点
上的点到焦点![]() 的最短距离为
的最短距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com