
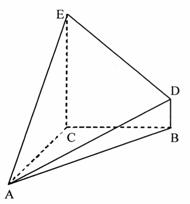
如图5所示,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,点
,点 在线段
在线段 上,
上, 平面
平面 .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)若 ,
, ,求二面角
,求二面角 的正切值.
的正切值.

 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
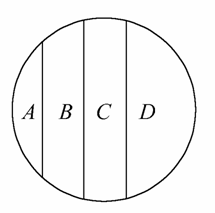
在一次随机试验中,彼此互斥的事件A、B、C、D的概率分别是0.2、0.2、0.3、0.3,则下列说法正确的是( )
A.A+B与C是互斥事件,也是对立事件
B.B+C与D是互斥事件,也是对立事件
C.A+C与B+D是互斥事件,但不是对立事件
D.A与B+C+D是互斥事件,也是对立事件
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}满足a1=1,a2=r(r>0),数列{bn}是公比为q的等比数列(q>0),bn=anan+1,cn=a2n-1+a2n,求cn。
查看答案和解析>>
科目:高中数学 来源: 题型:
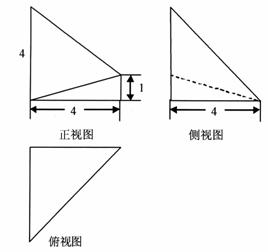
已知几何体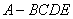 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(Ⅰ)求此几何体的体积;
(Ⅱ)求异面直线 与
与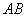 所成角的余弦值;
所成角的余弦值;
 (Ⅲ)探究在
(Ⅲ)探究在 上是否存在点Q,使得
上是否存在点Q,使得 ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
“单独二胎”政策的落实是我国完善计划生育基本国策的一项重要措施,事先需要做大量的调研论证.现为了解我市市民对该项措施是否认同,拟从全体市民中抽取部分样本进行调查.调查结果如下表:
| 调查人数 | 2 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 | 5000 |
| 认同人数 | 2 | 9 | 60 | 116 | 286 | 639 | 1339 | 1810 | 2097 | 4515 |
| 认同频率 | 1 | 0.9 | 0.857 | 0.892 | 0.922 | 0.913 | 0.893 | 0.905 | 0.899 | 0.903 |
则根据上表我们可以推断市民认同该项措施的概率最有可能为 ( )
A.0.80 B.0.85 C.0.90 D.0.92
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com