
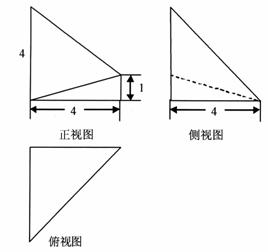
已知几何体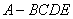 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(Ⅰ)求此几何体的体积;
(Ⅱ)求异面直线 与
与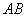 所成角的余弦值;
所成角的余弦值;
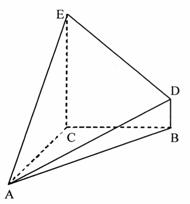 (Ⅲ)探究在
(Ⅲ)探究在 上是否存在点Q,使得
上是否存在点Q,使得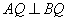 ,并说明理由.
,并说明理由.
解:(Ⅰ)由该几何体的三视图可知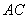 垂直于底面
垂直于底面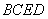 ,且
,且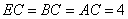 ,
, ,
,

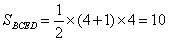 ,
,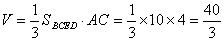 ,此几何体的体积为
,此几何体的体积为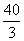 ;
;
解法一:(Ⅱ)过点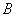 作
作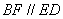 交
交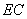 于
于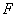 ,连接
,连接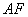 ,则
,则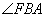 或其补角即为异面直线
或其补角即为异面直线 与
与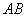 所成角,在
所成角,在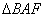 中,
中,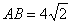 ,
,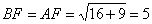 ,
,

 ;即异面直线
;即异面直线 与
与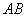 所成角的余弦值为
所成角的余弦值为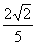 。
。
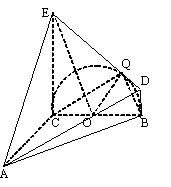 (Ⅲ)在
(Ⅲ)在 上存在点Q,使得
上存在点Q,使得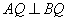 ;取
;取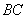 中点
中点 ,过点
,过点 作
作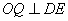 于点
于点 ,则点
,则点 为所求点;连接
为所求点;连接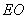 、
、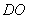 ,在
,在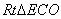 和
和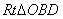 中,
中,

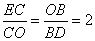 ,
,
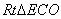 ∽
∽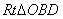 ,
,
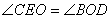 ,
,

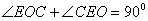 ,
,
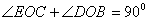 ,
,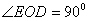 ,
,

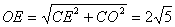 ,
,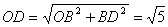 ,
,
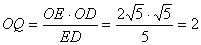 ,
,
 以
以 为圆心,
为圆心,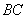 为直径的圆与
为直径的圆与 相切,切点为
相切,切点为 ,连接
,连接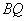 、
、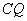 ,可得
,可得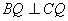 ;
;

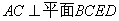 ,
,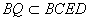 ,
,
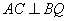 ,
,
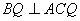 ,
,

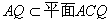 ,
,
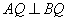 ;
;
解法二:(Ⅰ)同上。
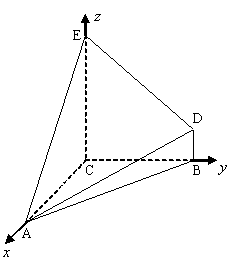 (Ⅱ)以
(Ⅱ)以 为原点,以
为原点,以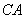 、
、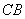 、
、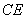 所在直线为
所在直线为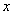 、
、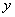 、
、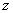 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则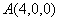 ,
,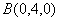 ,
,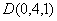 ,
,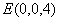 ,得
,得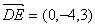 ,
,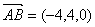 ,
,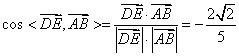 ,又异面直线
,又异面直线 与
与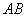 所成角为锐角,异面直线
所成角为锐角,异面直线 与
与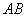 所成角的余弦值为
所成角的余弦值为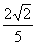 。
。
(Ⅲ)设存在满足题设的点 ,其坐标为
,其坐标为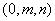 ,
,
则 ,
,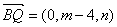 ,
,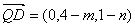 ,
,

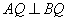 ,
,
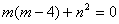 ①;
①;
 点
点 在
在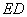 上,
上, 存在
存在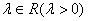 使得
使得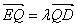 ,
,
即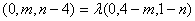 ,化简得
,化简得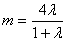 ,
,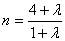 ②,
②,
②代入①得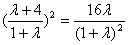 ,得
,得 ,
,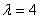 ;
;
 满足题设的点
满足题设的点 存在,其坐标为
存在,其坐标为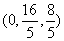 。
。


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
若△ 的三个内角满足
的三个内角满足 ,则△
,则△
(A)一定是锐角三角形. (B)一定是直角三角形.
(C)一定是钝角三角形. (D)可能是锐角三角形,也可能是钝角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
一袋中装有6个白球,3个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现9次停止.设停止时,取球次数为随机变量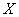 ,则
,则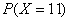 的值为( )
的值为( )
A.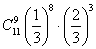 B.
B. 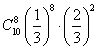 C.
C.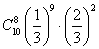 D.
D.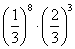
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com