在
中，内角A、B、C的对边长分别为
、
、
，已知
，且
求b 
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
已知数列{an}是公比q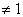
的等比数列，给出下列六个数列：（1）{kan}(k
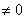) (2){a2n-1} (3){an+1-an} (4){anan+1} (5){nan} (6){an3},其中仍能构成等比数列的个数为
（A）4 （B）5 （C）6 （D）3 （ ）
查看答案和解析>>
科目：高中数学 来源： 题型：
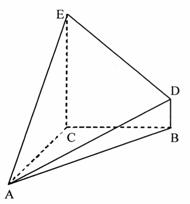
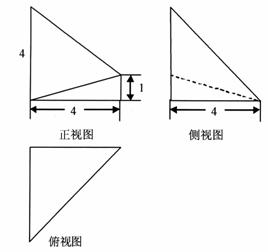
已知几何体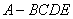
的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．
(Ⅰ)求此几何体的体积；
(Ⅱ)求异面直线
与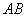
所成角的余弦值；
(Ⅲ)探究在上是否存在点Q，使得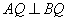
，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
如图，A,B,C,D都在同一个与水平面垂直的平面内，B，D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为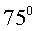
，
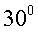，于水面C处测得B点和D点的仰角均为
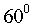，AC=0.1km。试探究图中B，D间距离与另外哪两点间距离相等，然后求B，D的距离（计算结果精确到0.01km，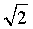
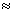1.414，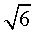
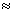2.449）
查看答案和解析>>
科目：高中数学 来源： 题型：
“单独二胎”政策的落实是我国完善计划生育基本国策的一项重要措施，事先需要做大量的调研论证．现为了解我市市民对该项措施是否认同,拟从全体市民中抽取部分样本进行调查．调查结果如下表：
| 调查人数 | 2 | 10 | 70 | 130 | 310 | 700 | 1500 | 2000 | 3000 | 5000 |
| 认同人数 | 2 | 9 | 60 | 116 | 286 | 639 | 1339 | 1810 | 2097 | 4515 |
| 认同频率 | 1 | 0．9 | 0．857 | 0．892 | 0．922 | 0．913 | 0．893 | 0．905 | 0．899 | 0．903 |
则根据上表我们可以推断市民认同该项措施的概率最有可能为 （ ）
A．0．80 B．0．85 C．0．90 D．0．92
查看答案和解析>>
科目：高中数学 来源： 题型：
某食品厂为了检查甲、乙两条自动包装流水线的生产情况，随机在这两条流水线上各抽取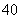
件产品作为样本．经统计，得到下列关于产品重量的样本频数分布表：
| 甲流水线 产品重量（单位：克） | 频数 | ||
| （490,495] | 2 | ||
| （495,500] | 12 | ||
| （500,505] | 18 | ||
| （505,510] | 6 | ||
| (510,515] | 2 | ||
| 乙流水线 产品重量（单位：克） | 频数 | ||
| （490,495] | 6 | ||
| （495,500] | 8 | ||
| （500,505] | 14 | ||
| （505,510] | 8 | ||
| （510,515] | 4 | ||
已知产品的重量合格标准为：重量值（单位：克）落在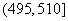
内的产品为合格品；否则为不合格品．
（Ⅰ) 从甲流水线样本的合格品中任意取2件，求重量值落在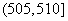
的产品件数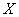
的分布列；
（Ⅱ）从乙流水线中任取2件产品，试根据样本估计总体的思想，求其中合格品的件数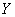
的数学期望；
（Ⅲ）从甲、乙流水线中各取2件产品，用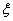
表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”，并用
表示事件“关于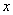
的一元二次方程
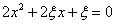没有实数解”． 试根据样本估计总体的思想，求事件的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
左侧是二次的右侧是一次的,学生总感觉用余弦定理不好处理,而对已知条件(2) 
过多
的关注两角
中则
由正弦定理及余弦定理有:
.又由已知
.解得
. 
的值；
的值；
是第三象限角，求
的值.
，
，则A=
（B）
（C）
（D）
∥
，求y的值，并求出向量