
 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润600元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润600元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.分析 (I)由题意先分段写出,当X∈[100,130)时,当X∈[130,150)时,和利润值,最后利用分段函数的形式进行综合即可.
(II)由(I)知,利润T不少于60000元,当且仅当110≤X≤150.再由直方图知需求量X∈[110,150]的频率为0.9,利用样本估计总体的方法得出下一个销售季度的利润T不少于60000元的概率的估计值.
解答 解:(I)由题意得,当X∈[100,130)时,
T=600X-300(130-X)=900X-39000,
当X∈[130,150)时,T=600×130=78000,
∴T=$\left\{{\begin{array}{l}{900X-39000}&{100≤X<130}\\{78000}&{130≤X≤150}\end{array}}\right.$;
(II)由(I)知,利润T不少于60000元,当且仅当110≤X≤150.
由直方图知需求量X∈[110,150]的频率为0.9,
下一个销售季度的利润T不少于60000元的概率的估计值为0.9.
点评 本题考查用样本的频率分布估计总体分布及识图的能力,求解的重点是对题设条件及直方图的理解,了解直方图中每个小矩形的面积的意义.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题

| A. | 6π+12 | B. | 6π+24 | C. | 12π+12 | D. | 24π+12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,\frac{1}{2}})$ | B. | $({\frac{1}{2},+∞})$ | C. | $({\frac{1}{4},\frac{1}{2}})$ | D. | $({-∞,\frac{1}{4}})∪({\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
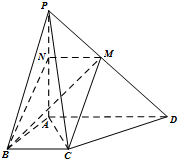 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com