
分析 先根据一元二次方程根的情况可判断f(3)一定是一个解,再假设f(x)的一解为A可得到x1+x2=6,同理可得到x3+x4=6,进而可得到x1+x2+x3+x4+x5=15,即可得到最后答案.
解答 解:对于f2(x)+bf(x)+c=2015来说,f(x)最多只有2解,
又f(x)=$\frac{1}{|x-3|}$(x≠3),函数关于x=3对称,当x不等于3时,x最多四解.
而题目要求5解,即可推断f(3)为一解,
假设f(x)的另一个解为A,得f(x)=$\frac{1}{|x-2|}$=A;
根据函数y═$\frac{1}{|x-3|}$的对称性得出:x1=3+A,x2=3-A,x1+x2=6;
同理:x3+x4=6;
所以:x1+x2+x3+x4+x5=6+6+3=15;
故答案为:15.
点评 本题主要考查一元二次方程根的情况和含有绝对值的函数的解法,考查基础知识的综合运用能力.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润600元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润600元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [0,4] | C. | {1,2,3,4} | D. | {0,1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
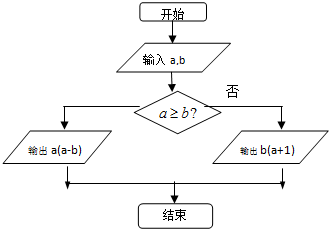
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com