
分析 (1)求导数,确定切线的斜率、切点坐标,即可求函数f(x)图象在点(1,f(1))处的切线方程;
(2)求导数,确定函数的单调性,即可求出函数f(x)最大值或最小值.
解答 解:(1)若a=2,f(x)=4lnx-x2.
∴f′(x)=$\frac{4}{x}$-2x,
∴f′(1)=2,
∵f(1)=-1,
∴函数f(x)图象在点(1,f(1))处的切线方程为y+1=2(x-1),即2x-y-3=0;
(2)f′(x)=$\frac{-2({x}^{2}-a)}{x}$,x>0.
由f′(x)>0,可得0$<x<\sqrt{a}$,函数单调递增,f′(x)<0,可得x$>\sqrt{a}$,函数单调递减,
∴函数f(x)在(0,+∞)上最大值为f($\sqrt{a}$)=alna-a,无最小值.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性与最值,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
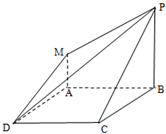 四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.
四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
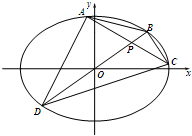 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两焦点坐标为$({-\sqrt{2},0}),({\sqrt{2},0})$,且过点$({\sqrt{2},1})$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两焦点坐标为$({-\sqrt{2},0}),({\sqrt{2},0})$,且过点$({\sqrt{2},1})$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com