
分析 (1)由题意可得,c1+c2=10,c2+c3=40,结合等比数列的通项公式可求公比q及c1,代入等比数列的通项公式可求cn,然后由cn=2an可求an,
(2)由bn=$\frac{1}{{{a_n}•{a_{n+1}}}}$=$\frac{1}{(2n-1)(2n+1)}$,考虑利用裂项求和即可求解Tn.
(3)假设否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,结合(2)代入可得 $\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$>0,解不等式可求m的范围,然后结合m∈N*,m>1可求.
解答 解:(1)解:由题意可得,c1+c2=10,c2+c3=c1q+c2q=40,
所以公比q=4,
∴c1+4c1=10
∴c1=2.
由等比数列的通项公式可得,cn=2•4n-1=22n-1.
∵cn=${2^{a_n}}$═22n-1
∴an=2n-1;
(2)∵bn=$\frac{1}{{{a_n}•{a_{n+1}}}}$=$\frac{1}{(2n-1)(2n+1)}$,
∴bn=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
于是Tn=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)]=$\frac{n}{2n+1}$.
(3)假设否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,
则( $\frac{m}{2m+1}$)2=$\frac{1}{3}$•$\frac{n}{2n+1}$.
可得$\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$>0,
由分子为正,解得1-$\frac{\sqrt{6}}{2}$<m<1+$\frac{\sqrt{6}}{2}$,
由m∈N*,m>1,得m=2,此时n=12,
当且仅当m=2,n=12时,T1,Tm,Tn成等比数列.
说明:只有结论,m=2,n=12时,T1,Tm,Tn成等比数列.
点评 本题主要考查了等比数列的通项公式的应用,数列的裂项求和方法的应用,属于数列知识的综合应用.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:解答题
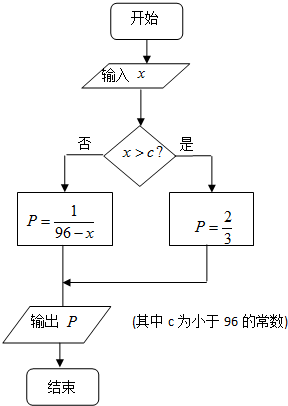 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{10}{3}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com