
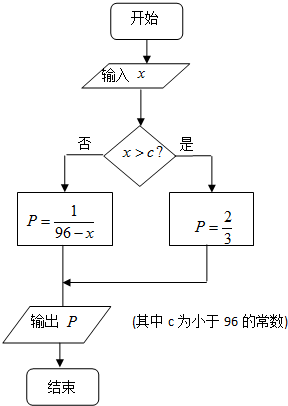
 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).分析 (Ⅰ)每天的赢利为T=日产量(x)×正品率(1-P)×盈利(A)-日产量(x)×次品率(P)×亏损,整理即可得到;
(Ⅱ)当x>c时,每天的盈利额T=0;当1≤c<84时,利用基本不等式可得x=c时,等号成立,利润最大;当84≤c<96时,当x=84时,利润最大.
解答 解:(Ⅰ)当1≤x≤c时,T=(1-$\frac{1}{96-x}$)xA-$\frac{1}{96-x}$xA=[x-$\frac{3x}{2(96-x)}$]A,
当x>c时,T=$\frac{1}{3}$xA-$\frac{2}{3}$x$\frac{A}{2}$=0,
$T=\left\{\begin{array}{l}[x-\frac{3x}{2(96-x)}]A\\ 0\end{array}\right.$$\begin{array}{l}{(1≤x≤c}&{x∈{N^*})}\\{(x>c}&{x∈{N^*})}\end{array}$…3分
(Ⅱ)(1)当x>c时,每天的盈利额T=0;
(2)当1≤x≤c且x∈N时,$T=[x-\frac{3x}{2(96-x)}]A$,
令96-x=t,则0<96-c≤t≤95(t∈N),
可得:$T=[96-t-\frac{3}{2}•\frac{96-t}{2t}]•A=(\frac{195}{2}-t-\frac{144}{t})A$,
令$g(t)=t+\frac{144}{t}$,
①当1≤c<84时,12<96-c<t≤95,g(t)在区间(12,95)为单增函数,
可得:$g{(t)_{min}}=g(96-c)=(96-c)+\frac{144}{96-c}$,$T≤[\frac{195}{2}-(96-C)-\frac{144}{96-C}]A=\frac{{189c-2{c^2}}}{192-2c}A>0$(当且仅当x=c时取等号),
∴当x=c时,Tmax=$\frac{189c-2{c}^{2}}{192-2c}$A,…9分
②当84≤c<96时,$g(t)≥2\sqrt{t•\frac{144}{t}=}24$,$T≤(\frac{195}{2}-24)A=\frac{147}{2}A>0$.
∴当t=12即x=84时,Tmax=$\frac{147}{2}$A
综上,当1≤c<84时,Tmax=$\frac{189c-2{c}^{2}}{192-2c}$A;84≤c<96时,Tmax=$\frac{147}{2}$A…12分
点评 本题考查了利润函数模型的应用,并且利用基本不等式求得函数的最值问题,也考查了分段函数的问题,是中档题.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1,-\frac{1}{3}$ | B. | $-1,\frac{1}{3}$ | C. | $1,-\frac{1}{3},0$ | D. | $-1,\frac{1}{3},0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
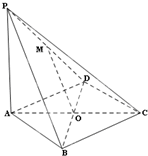 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
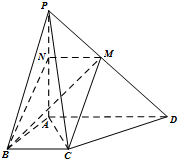 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m∥n | B. | m⊥n | C. | m、n异面 | D. | m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
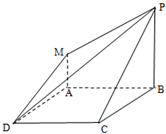 四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.
四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com