
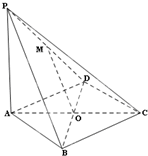
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.分析 (1)利用OM是△PDB的中位线来证明OM∥平面PAB;
(2)利用BD⊥AC,PA⊥BD证明DB⊥面PAC来证明平面PBD⊥平面PAC;
(3)以四边形ABCD为底面,列出体积等式,求出PA,在根据勾股定理来求PB长;
解答 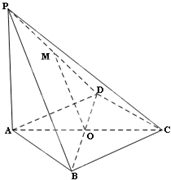 解:(1)在△PDB中,O、M分别是BD、PD的中点,
解:(1)在△PDB中,O、M分别是BD、PD的中点,
∴OM是△PDB的中位线,∴OM∥PB.
OM?面PBD,PB?面PDB,
∴OM∥面PBD.
(2)∵底面ABCD是菱形,
∴BD⊥AC,
∵PA⊥面ABCD,DB?面ABCD,
∴PA⊥BD;
∵AC?面PAC,PA?面PAC,AC∩PA=A
∴DB⊥面PAC,
∵BD?面PBD,
∴面PBD⊥面PAC.
(3)因为底面ABCD是菱形,AB=2,∠BAD=60°,所以SABCD=2$\sqrt{3}$.
∵四棱锥P-ABCD的高为PA,
∴$\frac{1}{3}×2\sqrt{3}×PA=\sqrt{3}$,得PA=$\frac{3}{2}$.
∵PA⊥面ABCD,AB?面ABCD,∴PA⊥AB.
在Rt△PAB中,PB=$\sqrt{P{A}^{2}+A{B}^{2}}$=$\sqrt{(\frac{3}{2})^{2}+{2}^{2}}$=$\frac{5}{2}$.
点评 本题主要考查了线面平行判定定理、面面垂直判定定理以及空间几何体体积,属中等题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
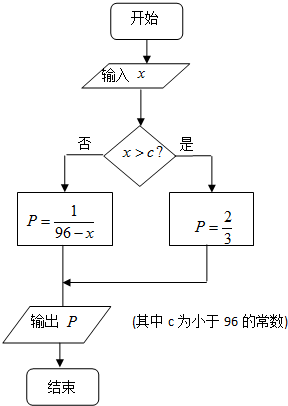 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com