
分析 (1)根据f′(-3)=0,求出a的值,从而求出函数的解析式,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(2)结合题意得到f'(x)≥0或者f'(x)≤0,通过讨论a的范围,结合二次函数的性质得到关于a的不等式,解出即可.
解答 解:(1)f'(-3)=0,得a=1.…(2分)
得f'(x)=x2+2x-3,令f'(x)=0,得x=-3,或x=1,…(4分)
在(-∞,-3),(1,+∞)上 f'(x)>0,
在(-3,1)上,f'(x)<0,
所以可知在x=1处有极小值,
${y_{极小值}}=f(1)=\frac{13}{3}$,…(6分)
(2)因为单调,所以f'(x)≥0或者f'(x)≤0,
f'(x)=ax2+(a+1)x-(a+2),
当a=0时,f'(x)=x-2,不符题意…..(8分)
当a≠0时,f'(x)=ax2+(a+1)x-(a+2)表示二次函数,
f'(x)≥0或者f'(x)≤0,所以与x轴有一个交点或者没有交点,
所以ax2+(a+1)x-(a+2)=0至多一个根,
所以△≤0,所以$\frac{{-5-2\sqrt{5}}}{5}≤a≤\frac{{-5+2\sqrt{5}}}{5}$…(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,转化思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
 如图,A,B,C,H四个小朋友在草坪上游戏,根据游戏规则,A,B,C三人围成一个三角形,B,H,C三人共线,H在B,C两人之间.B,C两人相距10m,A,H两人相距hm,AH与BC垂直.
如图,A,B,C,H四个小朋友在草坪上游戏,根据游戏规则,A,B,C三人围成一个三角形,B,H,C三人共线,H在B,C两人之间.B,C两人相距10m,A,H两人相距hm,AH与BC垂直.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2{e}^{2}}$,$\frac{1}{e}$) | B. | ($\frac{1}{{e}^{2}}$,$\frac{1}{e}$) | C. | (e,2e) | D. | (e,e3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示.成绩落在[70,80)中的人数为20.
为了了解某学校高二年级学生的物理成绩,从中抽取n名学生的物理成绩(百分制)作为样本,按成绩分成 5组:[50,60),[60,70),[70,80),[80,90),[90,100],频率分布直方图如图所示.成绩落在[70,80)中的人数为20.| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k) | 0.50 | 0.05 | 0.025 | 0.005 |
| k | 0.455 | 3.841 | 5.024 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
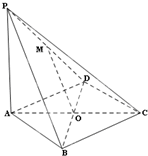 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com