
分析 由题意知采用系统抽样和分层抽样方法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,算出总体个数,根据分层抽样的比例和抽取的工程师人数得到n应是6的倍数,36的约数,由系统抽样得到$\frac{35}{n+1}$必须是整数,验证出n的值.
解答 解:由题意知采用系统抽样和分层抽样方法抽取,不用剔除个体;
如果样本容量增加一个,则在采用系统抽样时,
需要在总体中先剔除1个个体,
∵总体容量为6+12+18=36.
当样本容量是n时,由题意知,系统抽样的间隔为$\frac{36}{n}$,
分层抽样的比例是$\frac{n}{36}$,抽取的工程师人数为$\frac{n}{36}$•6=$\frac{n}{6}$,
技术员人数为$\frac{n}{36}$•12=$\frac{n}{3}$,技工人数为$\frac{n}{36}$•18=$\frac{n}{2}$,
∵n应是6的倍数,36的约数,
即n=6,12,18.
当样本容量为(n+1)时,总体容量是35人,
系统抽样的间隔为$\frac{35}{n+1}$,
∵$\frac{35}{n+1}$必须是整数,
∴n只能取6.
即样本容量n=6.
工程师晏某被抽中的概率为$\frac{6}{36}$=$\frac{1}{6}$.
故答案为6,$\frac{1}{6}$.
点评 本题考查分层抽样和系统抽样,是一个用来认识这两种抽样的一个题目,把两种抽样放在一个题目中考查,加以区分,是一个好题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5π | B. | 13π | C. | 17π | D. | 25π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | $±\sqrt{2}$ | C. | $±\frac{{\sqrt{2}}}{2}$ | D. | $±\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
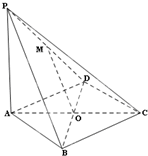 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=1,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | 若“a>b”,则“a•c>b•c” | |
| C. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” | |
| D. | 一个命题的否命题为真,则它的逆命题一定为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -6 | C. | 11 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com