练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．已知点A（0，2）和抛物线C：y2=6x，求过点A且与抛物线C只有一个交点的直线l的方程．

    分析 分两种情况讨论：（1）当该直线存在斜率时；（2）该直线不存在斜率时，即可得出结论．

    解答 解：（1）当过点P（0，2）的直线存在斜率时，设其方程为：y=kx+2，
    代入抛物线方程，消y得k2x2+（4k-6）x+4=0，
    ①若k=0，方程为y=2，此时直线与抛物线只有一个交点；
    ②若k≠0，令△=（4k-6）2-16k2=0，解得k=$\frac{3}{4}$，此时直线与抛物线相切，只有一个交点，
    此时直线方程为3x-4y+8=0；
    （2）当过点P（0，2）的直线不存在斜率时，该直线方程为x=0，与抛物线相切只有一个交点；
    综上，过点P（0，2）与抛物线y2=6x有且只有一个交点的直线方程为y=2，x=0和3x-4y+8=0．

    点评 本题考查了直线与圆锥曲线的关系，考查了分类讨论的数学思想方法，训练了利用判别式判断一元二次方程解的个数，是中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．为了了解某学校高二年级学生的物理成绩，从中抽取n名学生的物理成绩（百分制）作为样本，按成绩分成 5组：[50，60），[60，70），[70，80），[80，90），[90，100]，频率分布直方图如图所示．成绩落在[70，80）中的人数为20．
    男生女生合计
    优秀
    不优秀
    合计
    （Ⅰ）求a和n的值；
    （Ⅱ）根据样本估计总体的思想，估计该校高二学生物理成绩的平均数$\overline x$和中位数m；
    （Ⅲ）成绩在80分以上（含80分）为优秀，样本中成绩落在[50，80）中的男、女生人数比为1：2，成绩落在[80，100]中的男、女生人数比为3：2，完成2×2列联表，并判断是否有95%的把握认为物理成绩优秀与性别有关．
    参考公式和数据：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
    P（K2≥k）0.500.050.0250.005
    k0.4553.8415.0247.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

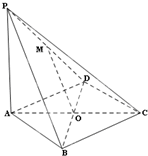    19．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，M是PD的中点，AB=1，∠BAD=60°．
    （1）求证：OM∥平面PAB；
    （2）平面PBD⊥平面PAC；
    （3）当三棱锥C-PBD的体积等于$\frac{\sqrt{3}}{2}$时，求PB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知m，n是两条不同的直线，α、β是两个不同的平面，若m?α，n?β，且α∥β，则下列结论一定正确的是（　　）
    A．m∥nB．m⊥nC．m、n异面D．m∥β

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知函数f（x）=mx3+nx+1（mn≠0），且f（-1）=5，则f（1）=7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

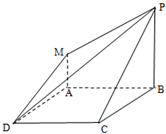    13．四边形ABCD是正方形，PB⊥平面ABCD，MA∥PB，PB=AB=2MA．
    （1）求直线BD与平面PCD所成的角；
    （2）求平面PMD与平面ABCD所成角的大小的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．三棱锥P-ABC中，PA⊥面ABC，AB⊥AC，AB=1，AC=1，PA=$\sqrt{2}$，该三棱锥外接球表面积为（　　）
    A．16πB．$\frac{4}{3}π$C．πD．4π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数$f（x）=sinx+2xf'（\frac{π}{4}）+1$，则${f^/}（\frac{π}{3}）$=$\frac{1-2\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．观察下列不等式：
    $\begin{array}{l}\frac{1}{5}＜\frac{1}{4}，\\ \frac{1}{5}+\frac{1}{13}＜\frac{1}{3}\\ \frac{1}{5}+\frac{1}{13}+\frac{1}{25}＜\frac{3}{8}\\ \frac{1}{5}+\frac{1}{13}+\frac{1}{25}+\frac{1}{41}＜\frac{2}{5}\\…\end{array}$
    则第n个不等式为$\frac{1}{5}+\frac{1}{13}+…+\frac{1}{2{n}^{2}+2n+1}$＜$\frac{n}{2n+2}$．

    查看答案和解析>>

    同步练习册答案