
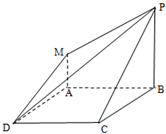
 四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.
四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.分析 (1)由已知中PB⊥平面ABCD,CD⊥BC,我们结合线面垂直的性质及判定可得CD⊥平面PBC,再由面面垂直的判定可得面PBC⊥平面PCD,过B作BF⊥PC于F,连DF,易得∠BDF是直线BD与平面PDC所成的角,解三角形BDF,即可求出直线BD与平面PCD所成的角的大小;
(2)分别延长PM,BA,设PM∩BA=G,连DG,过A作AN⊥DG于N,连MN,.则∠MNA是平面PMD与平面ABCD所成的二面角的平面角,解三角形MNA,即可求出平面PMD与平面ABCD所成的二面角(锐角)的正切值.
解答 解:(1)如图,PB⊥平面ABCD,CD?平面ABCD,
∴CD⊥PB.
又∵CD⊥BC,
∴CD⊥平面PBC、
∵CD?平面PCD,
∴平面PBC⊥平面PCD、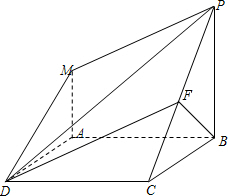
过B作BF⊥PC于F,则BF⊥平面PDC,连DF,则DF为BD在平面PCD上的射影.
∴∠BDF是直线BD与平面PDC所成的角.
不妨设AB=2,则在Rt△PBC中,PB=BC=2,BF⊥PC,
∴BF=$\frac{1}{2}$PC=$\sqrt{2}$.
∵BD=2$\sqrt{2}$.
∴在Rt△BFD中,BF=$\frac{1}{2}$BD,
∴∠BDF=$\frac{π}{6}$.
∴直线BD与平面PCD所成的角是$\frac{π}{6}$.
(2)如图,
分别延长PM,BA,设PM∩BA=G,连DG,
则平面PMD∩平面ABCD=DG.
不妨设AB=2,
∵MA∥PB,PB=2MA,
∴GA=AB=2.
过A作AN⊥DG于N,连MN.
∵PB⊥平面ABCD,
∴MA⊥平面ABCD,∴MN⊥DG.
∴∠MNA是平面PMD与平面ABCD
所成的二面角的平面角(锐角).
在Rt△MAN中,
tan∠MNA=$\frac{MA}{NA}$=$\frac{\sqrt{2}}{2}$.
∴平面PMD与平面ABCD所成的二面角的正切值是$\frac{\sqrt{2}}{2}$.
点评 本题考查的知识点是二面角的平面角及求示,直线与平面所成的角,其中在求线面夹角及二面角时,找出其平面角是解答此类问题的关键.


科目:高中数学 来源: 题型:解答题
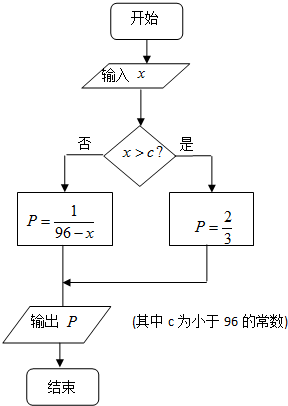 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [0,4] | C. | {1,2,3,4} | D. | {0,1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{10}{3}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com