
分析 (1)由Sn=n2+2n(n∈N+).可得n=1时,b1=3;n≥2时,bn=Sn-Sn-1.
(2)由(1)可得$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$.利用“裂项求和方法”即可得出.
解答 解:(1)∵Sn=n2+2n(n∈N+).∴n=1时,b1=3;n≥2时,bn=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1.
n=1时也成立,∴bn=2n+1.
(2)由(1)可得$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}(\frac{1}{2n+1}-\frac{1}{2n+3})$.
∴数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Tn=$\frac{1}{2}$$[(\frac{1}{3}-\frac{1}{5})$+$(\frac{1}{5}-\frac{1}{7})$+…+$(\frac{1}{2n+1}-\frac{1}{2n+3})]$
=$\frac{1}{2}(\frac{1}{3}-\frac{1}{2n+3})$,
∴${T_n}=\frac{n}{6n+9}$.
点评 本题考查了数列递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
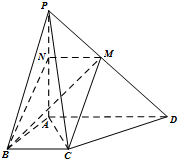 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m∥n | B. | m⊥n | C. | m、n异面 | D. | m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
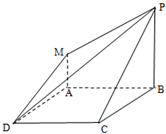 四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.
四边形ABCD是正方形,PB⊥平面ABCD,MA∥PB,PB=AB=2MA.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com