
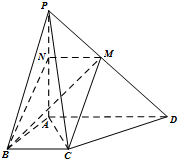
 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).分析 (Ⅰ)证明BC∥平面PAD,利用线面平行的性质定理证明MN∥BC;
(Ⅱ)过M作MK∥PA交AD于K,连结BK,证明AC⊥BK.知$AK=\frac{1}{3}AD$,即可求此时$\frac{PM}{PD}$的值.
解答 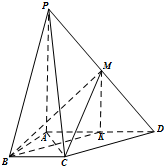 (Ⅰ)证明:因为梯形ABCD,且BC∥AD,
(Ⅰ)证明:因为梯形ABCD,且BC∥AD,
又因为BC?平面PAD,AB?平面PAD,
所以BC∥平面PAD.
因为平面BCNM∩平面PAD=MN,
所以MN∥BC. …(4分)
(Ⅱ)解:过M作MK∥PA交AD于K,连结BK.
因为PA⊥底面ABCD,
所以MK⊥底面ABCD
所以MK⊥AC.
又因为BM⊥AC,BM∩MK=M
所以AC⊥平面BMK,
所以AC⊥BK.
知$AK=\frac{1}{3}AD$,
所以$\frac{PM}{PD}=\frac{1}{3}$. …(12分)
点评 本题考查线面平行的判定与性质,考查线面垂直,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润600元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润600元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
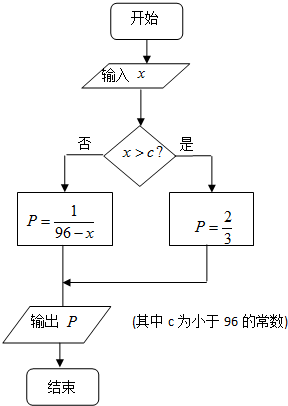 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率P与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率$P=\frac{次品数}{生产量}$,如P=0.1表示每生产10件产品,约有1件次品,其余为合格品).又已知每生产一件合格的仪器可以盈利A(元),但每生产一件次品将亏损$\frac{A}{2}$(元).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
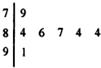 在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )
在某校举办的“激扬青春,勇担责任”演讲比赛中,有七位评委选手打分,若选手甲所得分数用茎叶图表示如图,则选手甲所得分数的中位数为( )| A. | 87 | B. | 86 | C. | 85 | D. | 84 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [0,4] | C. | {1,2,3,4} | D. | {0,1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com