
分析 分别解关于A、B的不等式,(1)根据集合的运算性质求出A、B的交集以及A、B的并集,从而求出其补集;(2)根据集合的包含关系得到关于a的不等式组,解出即可.
解答 解:A={x|x2-6x+5<0}=(1,5),
B=$\left\{{\left.x\right|\frac{x-2}{x-4}>0}\right\}$={x|x>4或x<2},
C={x|3a-2<x<4a-3}
(1)A∩B=(1,2)∪(4,5),
A∪B=R,∁U(A∪B)=∅;
(2)若C⊆A,则$\left\{\begin{array}{l}{3a-2≥1}\\{4a-3≤5}\end{array}\right.$,
解得:1≤a≤2.
点评 本题考查了集合的运算,考查不等式问题,是一道基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,\frac{1}{2}})$ | B. | $({\frac{1}{2},+∞})$ | C. | $({\frac{1}{4},\frac{1}{2}})$ | D. | $({-∞,\frac{1}{4}})∪({\frac{1}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1,-\frac{1}{3}$ | B. | $-1,\frac{1}{3}$ | C. | $1,-\frac{1}{3},0$ | D. | $-1,\frac{1}{3},0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 78 16 65 72 08 02 63 14 07 02 43 69 69 38 74 |
| 32 04 94 23 49 55 80 20 36 35 48 69 97 28 01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
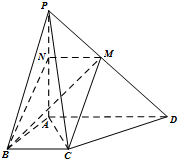 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{3}$AD,PA⊥底面ABCD,过AB的平面交PD于AB,交PC于N(N与A不重合).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com