
分析 (1)m=a+$\frac{1}{(a-b)b}$=(a-b)+b+$\frac{1}{(a-b)b}$,结合基本不等式,可得m的最小值t;
(2)由柯西不等式得:[x2+(2y)2+z2](12+12+12)≥(x+2y+z)2,进而可证得:|x+2y+z|≤3.
解答 解:(1)由三个数的均值不等式得:
$m=(a-b)+b+\frac{1}{(a-b)b}≥3\root{3}{{(a-b)b•\frac{1}{(a-b)b}}}=3$
(当且仅当$a-b=b=\frac{1}{a-b}$即b=1,a=2时取“=”号),
故有t=3. (5分)
证明:(2)∵x2+4y2+z2=3,由柯西不等式得:[x2+(2y)2+z2](12+12+12)≥(x+2y+z)2
(当且仅当$\frac{x}{1}=\frac{2y}{1}=\frac{z}{1}$即$x=z=\frac{6}{5},y=\frac{3}{5}$时取“=”号)
整理得:(x+2y+z)2≤9,即|x+2y+z|≤3. (10分)
点评 本题考查的知识点是基本不等式和柯西不等式,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
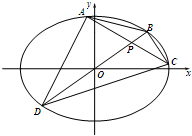 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两焦点坐标为$({-\sqrt{2},0}),({\sqrt{2},0})$,且过点$({\sqrt{2},1})$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的两焦点坐标为$({-\sqrt{2},0}),({\sqrt{2},0})$,且过点$({\sqrt{2},1})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既有最大值又有最小值的奇函数 | B. | 最大值为2的偶函数 | ||
| C. | 最大值为1.5的偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-1,3) | C. | (3,1) | D. | (-3,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com