
分析 设t=f(x),作出函数f(x)的图象,根据关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解x1,x2,x3,得到t的取值情况即可求出结论.
解答 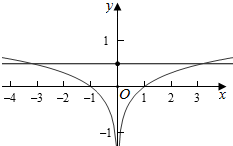 解:设t=f(x),则关于x的方程f2(x)+bf(x)+c=0等价为t2+bt+c=0,
解:设t=f(x),则关于x的方程f2(x)+bf(x)+c=0等价为t2+bt+c=0,
作出f(x)的图象如图:
由图象可知当t=$\frac{1}{2}$时,方程f(x)=$\frac{1}{2}$有三个根,当t≠$\frac{1}{2}$时方程f(x)=t有两个不同的实根,
∴若关于x的方程f2(x)+bf(x)+c=0恰有3个不同的实数解x1,x2,x3,
则等价为t2+bt+c=0只有一个根t=$\frac{1}{2}$,
由f(x)=$\frac{1}{2}$得,x=0,或者lg|x|=$\frac{1}{2}$,
即得x=±10${\;}^{\frac{1}{2}}$=±$\sqrt{10}$,
即三个根x1,x2,x3,分别为0,$\sqrt{10}$或-$\sqrt{10}$,
∴x12+x22+x32═0+10+10=20.
故答案为:20.
点评 本题主要考查方程根的个数的应用,利用换元法将方程转化为二次方程,根据二次方程根的分布是解决本题的关键,利用数形结合是解决本题的基本思想.


科目:高中数学 来源: 题型:解答题
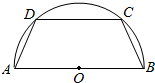 如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.
如图,有一块半径为2的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,写出这个梯形的周长y和腰长x之间的函数解析式,并求出它的定义域.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?n∈N,n2≤2n | B. | ?n∈N,n2<2n | C. | ?n∈N,n2≤2n | D. | ?n∈N,n2<2n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
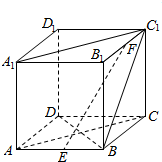 已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.
已知ABCD-A1B1C1D1为正方体,E、F分别是AB、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | (2,4) | C. | (6,9) | D. | (7,9) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com