
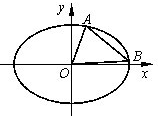
如图,椭圆C:x2+3y2=3b2(b>0).

(Ⅰ)求椭圆C的离心率;
(Ⅱ)若b=1,A,B是椭圆C上两点,且|AB|=![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
|
(Ⅰ)解:由x2+3y2=3b2 得 所以e= (Ⅱ)解:设A(x1,y1),B(x2,y2),△ABO的面积为S. 如果AB⊥x轴,由对称性不妨记A的坐标为( 如果AB不垂直于x轴,设直线AB的方程为y=kx+m, 由 即(1+3k2)x2+6kmx+3m2-3=0,又Δ=36k2m2-4(1+3k2)(3m2-3)>0, 所以x1+x2=- (x1-x2)2=(x1+x2)2-4x1x2= 由|AB|= (x1-x2)2= 结合①,②得m2=(1+3k2)- 所以S= 因此S2= =- 故S≤ |
|
本题主要考查椭圆的几何性质,直线与椭圆的位置关系等基础知识,同时考查解析几何的基本思想方法和综合解题能力.满分15分. |


科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•石景山区二模)如图,椭圆C:x2+
(2013•石景山区二模)如图,椭圆C:x2+| y2 |
| m |
| 9 |
| 5 |
4
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
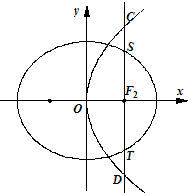 如图,椭圆E:
如图,椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| |CD| |
| |ST| |
| 6 |
| PE |
| PF |
查看答案和解析>>
科目:高中数学 来源:湖南省长郡中学2012届高三第五次月考数学理科试题 题型:044
如图,椭圆C:x2+3y2=3b2(b>0).

(1)求椭圆C的离心率;
(2)若b=1,A,B是椭圆C上的两点,且|AB|=![]() ,求△AOB面积的最大值.
,求△AOB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com