解:(1)由已知,动点M到定点F(0,

)的距离比它到x轴的距离大

,
∴动点M到定点F(0,

)的距离等于它到定直线

的距离,…(2分)
∴动点M的轨迹曲线E是顶点在原点,焦点为F(0,

)的抛物线和点(0,-

)…(4分)
∴曲线E的轨迹方程为x
2=y和y=-

(x=0).…(6分)
(2)由

,解得

或
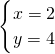
…(8分)
即A(-1,1),B(2,4)
设过原点与点A、B的圆C的方程为x
2+y
2+Dx+Ey+F=0,
则

,解得
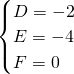
∴圆C的方程为x
2+y
2-2x-4y=0,即(x-1)
2+(y-2)
2=5 …(10分)
由上可知,过点M(0,4)且与直线l垂直的直线MM′方程为:y=-x+4
解方程组
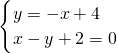
,得

,即线段MM′中点坐标为H(1,3)…(12分)
从而得点M(0,4)关于直线l的对称点M′的坐标为M′(2,2)
把M′(2,2)代入,可得(x-1)
2+(y-2)
2≠5
∴点M′(2,2)不在圆C上.…(14分)
分析:(1)由动点M到定点F(0,

)的距离比它到x轴的距离大

,可得动点M到定点F(0,

)的距离等于它到定直线

的距离,从而可得曲线E的轨迹方程;
(2)由

,求得A,B的坐标,假设过原点与点A、B的圆C的方程为x
2+y
2+Dx+Ey+F=0,代入可得圆C的方程,求出点M(0,4)关于直线l的对称点M′的坐标,代入验证,即可得到结论.
点评:本题主要考查直线与圆锥曲线的综合应用能力,涉及到轨迹方程的求法及直线与抛物线的相关知识,考查运算求解能力,推理论证能力

 )的距离比它到x轴的距离大
)的距离比它到x轴的距离大 ,设动点M的轨迹是曲线E.
,设动点M的轨迹是曲线E. )的距离比它到x轴的距离大
)的距离比它到x轴的距离大 ,
, )的距离等于它到定直线
)的距离等于它到定直线 的距离,…(2分)
的距离,…(2分) )的抛物线和点(0,-
)的抛物线和点(0,- )…(4分)
)…(4分) (x=0).…(6分)
(x=0).…(6分) ,解得
,解得 或
或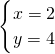 …(8分)
…(8分) ,解得
,解得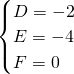
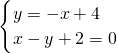 ,得
,得 ,即线段MM′中点坐标为H(1,3)…(12分)
,即线段MM′中点坐标为H(1,3)…(12分) )的距离比它到x轴的距离大
)的距离比它到x轴的距离大 ,可得动点M到定点F(0,
,可得动点M到定点F(0, )的距离等于它到定直线
)的距离等于它到定直线 的距离,从而可得曲线E的轨迹方程;
的距离,从而可得曲线E的轨迹方程; ,求得A,B的坐标,假设过原点与点A、B的圆C的方程为x2+y2+Dx+Ey+F=0,代入可得圆C的方程,求出点M(0,4)关于直线l的对称点M′的坐标,代入验证,即可得到结论.
,求得A,B的坐标,假设过原点与点A、B的圆C的方程为x2+y2+Dx+Ey+F=0,代入可得圆C的方程,求出点M(0,4)关于直线l的对称点M′的坐标,代入验证,即可得到结论.

 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.