解:∵一颗骰子投掷两次,记第一次出现的点数为a
2,第二次出现的点数为b
2
∴(a
2,b
2)所有可能的情况是(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6);(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2、6);(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3、6);(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4、6);(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5、6);(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6、6),共有36种.…(2分)
(Ⅰ)设事件A表示“焦点在x轴上的椭圆”,方程

表示焦点在x轴上的椭圆,则a
2>b
2,且a
2>b
2的所有可能的情况是(2,1)、(3,1)、(3,2)、(4,1)、(4,2)、(4,3)、(5,1)、(5,2)、(5,3)、(5,4)(6,1)、(6,2)、
(6,3)、(6,4)、(6,5)共有15种.所以
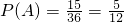
;…(7分)
(Ⅱ)设事件B表示“离心率为2的双曲线”,即
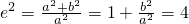
,
所以
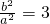
,则满足条件的有(1,3),(2,6)共有2种.
∴
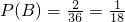
. …(12分)
分析:先确定事件的所有可能情况,再分别计算
(Ⅰ)方程

表示焦点在x轴上的椭圆,则a
2>b
2,且a
2>b
2的所有可能的情况,即可求得结论;
(Ⅱ)方程

表示离心率为2的双曲线,则
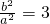
,满足条件的有(1,3),(2,6)共有2种,故可得结论.
点评:本题以圆锥曲线为载体,考查概率知识的运用,解题的关键是确定基本事件的个数.

 表示焦点在x轴上的椭圆的概率;
表示焦点在x轴上的椭圆的概率; 表示离心率为2的双曲线的概率.
表示离心率为2的双曲线的概率. 表示焦点在x轴上的椭圆,则a2>b2,且a2>b2的所有可能的情况是(2,1)、(3,1)、(3,2)、(4,1)、(4,2)、(4,3)、(5,1)、(5,2)、(5,3)、(5,4)(6,1)、(6,2)、
表示焦点在x轴上的椭圆,则a2>b2,且a2>b2的所有可能的情况是(2,1)、(3,1)、(3,2)、(4,1)、(4,2)、(4,3)、(5,1)、(5,2)、(5,3)、(5,4)(6,1)、(6,2)、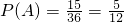 ;…(7分)
;…(7分)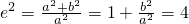 ,
,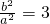 ,则满足条件的有(1,3),(2,6)共有2种.
,则满足条件的有(1,3),(2,6)共有2种.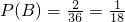 . …(12分)
. …(12分) 表示焦点在x轴上的椭圆,则a2>b2,且a2>b2的所有可能的情况,即可求得结论;
表示焦点在x轴上的椭圆,则a2>b2,且a2>b2的所有可能的情况,即可求得结论; 表示离心率为2的双曲线,则
表示离心率为2的双曲线,则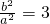 ,满足条件的有(1,3),(2,6)共有2种,故可得结论.
,满足条件的有(1,3),(2,6)共有2种,故可得结论.
