
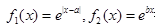
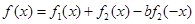 ,是否存在a,b
,是否存在a,b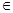 R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;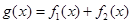 在R上的单调区间;
在R上的单调区间;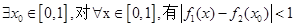 成立.求a的取值范围.
成立.求a的取值范围.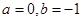 使
使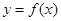 为偶函数〔II)
为偶函数〔II)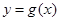 的增区间为
的增区间为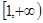 ,减区间为
,减区间为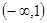 。(III )
。(III )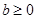 时,
时,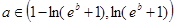 ;当
;当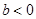 时,
时,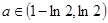
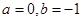 使
使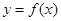 为偶函数,………………(2分)
为偶函数,………………(2分)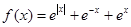 ,
,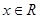
 ,
,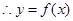 为偶函数。………………(4分)
为偶函数。………………(4分)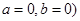 也可以)
也可以)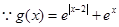 =
=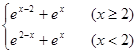 ,………………(5分)
,………………(5分)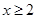 时
时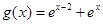 ,
,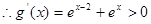
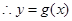 在
在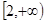 上为增函数。………………(6分)
上为增函数。………………(6分)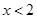 时
时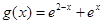 ,
,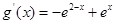 ,令
,令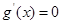 得到
得到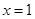 ,
,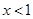 时
时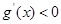 ,
,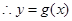 在
在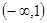 上为减函数。
上为减函数。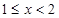 时
时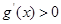 ,
,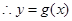 在
在 上为增函数。………………(8分)
上为增函数。………………(8分)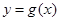 的增区间为
的增区间为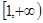 ,减区间为
,减区间为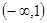 。………………(9分)
。………………(9分) ,
,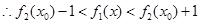
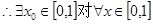 ,
,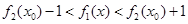 成立。
成立。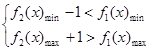 …………………………………………………(10分)
…………………………………………………(10分)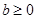 时,
时,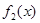 为增函数或常数函数,
为增函数或常数函数,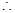 当
当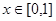 时
时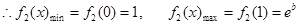
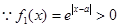
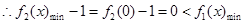 恒成立。
恒成立。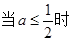
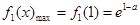
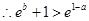
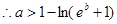
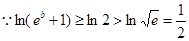
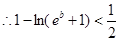
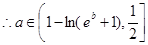
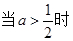
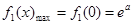
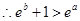

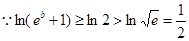
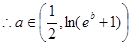
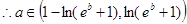 ……………………………………………(12分)
……………………………………………(12分)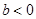 时,
时,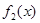 在[0,1]上为减函数,
在[0,1]上为减函数,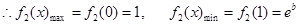
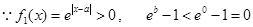
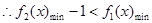 恒成立。
恒成立。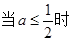
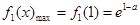
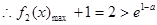
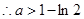
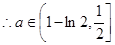
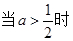
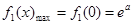
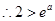
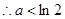
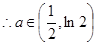
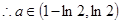 ……………………………………………(13分)
……………………………………………(13分)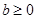 时,
时,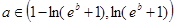 ;
;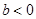 时,
时,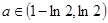 .……………………………………………(14分)
.……………………………………………(14分)

 习题精选系列答案
习题精选系列答案科目:高中数学 来源:不详 题型:解答题
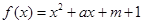 ,关于x的不等式
,关于x的不等式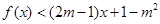 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设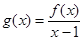 .
.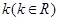 如何取值时,函数
如何取值时,函数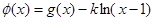 存在极值点,并求出极值点;
存在极值点,并求出极值点;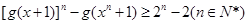
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.f(0)<0 | B.f(1)>0 |
| C.f(1)>f(0) | D.f(1)<f(0) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
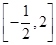 上只有一个零点,求实数a的取值范围.
上只有一个零点,求实数a的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com