练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．设全集U={0，1，2，3}，集合A={0，1，2}，集合B={2，3}，则（∁UA）∪B=（　　）
    A．∅B．{1，2，3}C．{0，1，2，3}D．{2，3}

    分析 由全集U及A，求出A的补集，找出A补集与B的并集即可．

    解答 解：∵全集U={0，1，2，3}，A={0，1，2}，B={2，3}，
    ∴∁UA={3}，
    则（∁UA）∪B={2，3}，
    故选：D．

    点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

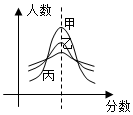    9．某市期末教学质量检测，甲、乙、丙三科考试成绩近似服从正态分布，则由如图曲线可得下列说法中错误的是（　　）
    A．甲、乙、丙的总体的均值都相同B．甲学科总体的方差最小
    C．乙学科总体的方差及均值都居中D．丙学科总体的方差最大

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．$\int_0^2{（{x-1}）dx=}$（　　）
    A．-1B．1C．0D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知$\overrightarrow{m}$=（sinωx，cosωx），$\overrightarrow{n}$=（cosωx，cosωx）其中ω＞0，若函数f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$-$\frac{1}{2}$的图象上相邻两对称轴间得距离为2π
    （1）求方程f（x）-$\frac{\sqrt{6}}{4}$=0在区间[0，17]内的解；
    （2）若$\overrightarrow{m}$•$\overrightarrow{n}$=$\frac{1}{2}$+$\frac{\sqrt{2}}{4}$，求sinx；
    （3）在△ABC中，a，b，c分别是角A，B，C的对边，且满足（2a-c）cosB=bcosC，求函数f（A）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．设函数y=f（x）在区间[0，1]上的图象是连续不断的一条曲线，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算出曲线y=f（x）及直线x=0，x-1=0，y=0所围成部分的面积S．先产生两组（每组100个）区间[0，1]上的均匀随机数x1，x2，x3，…x100和y1，y2，y3，…，y100，由此得到100个点（xi，yi）（i=1，2，3，…100），若发现其中满足yi＞f（xi）（i=1，2，3，…100）的点有32个，那么由随机方法可以得到S的近似值为$\frac{8}{25}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．若正数x，y满足x+3y=5xy，求：
    （1）3x+4y的最小值；
    （2）求xy的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．以点（2，-2）为圆心并且与圆x2+y2+2x-4y+1=0相外切的圆的方程是（　　）
    A．（x+2）2+（y+2）2=9B．（x-2）2+（y+2）2=9C．（x-2）2+（y-2）2=16D．（x-2）2+（y+2）2=16

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．直线y=a分别与直线y=3x+3，曲线y=2x+lnx交于A，B两点，则|AB|的最小值为$\frac{4}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知x，y为正实数，则$\frac{2x}{x+2y}$+$\frac{y}{x}$的最小值为$\frac{3}{2}$．

    查看答案和解析>>

    同步练习册答案