
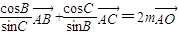 ,则m=( )
,则m=( )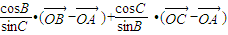 =
=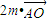 ,左右分别与
,左右分别与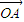 作数量积,化简可得 sin(B+C)=m,再利用诱导公式可得m=sinA=sinθ,从而得出结论.
作数量积,化简可得 sin(B+C)=m,再利用诱导公式可得m=sinA=sinθ,从而得出结论.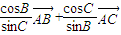 =
=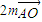 可化为:
可化为: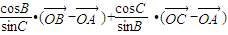 =
=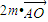 (*).
(*).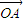 与
与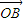 的夹角为2∠C,
的夹角为2∠C,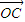 与
与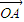 的夹角为2∠B,
的夹角为2∠B,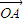 与
与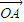 的夹角为0,
的夹角为0,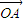 |=|
|=|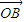 |=|
|=|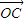 |=R.
|=R.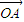 作数量积,可得:
作数量积,可得: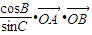 -
-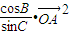 +
+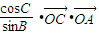 -
-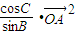 =-2m
=-2m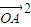 .
. R2 (cos2C-1)+
R2 (cos2C-1)+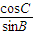 •R2(cos2B-1)=-2mR2.
•R2(cos2B-1)=-2mR2.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| cosB |
| sinC |
| AB |
| cosC |
| sinB |
| AC |
| AO |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| cosB |
| sinC |
| AB |
| cosC |
| sinB |
| AC |
| AO |
| A.sinθ | B.cosθ | C.tanθ | D.不能确定 |
查看答案和解析>>
科目:高中数学 来源:2011年上海市黄浦区大同中学高考数学专项训练:三角函数(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com