
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]() .
.
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)若![]() ,且数列
,且数列![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,数列
,数列![]() 满足:
满足:![]() 对于任意给定的正整数
对于任意给定的正整数![]() ,是否存在
,是否存在![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的值(只要写出一组即可);若不存在,说明理由.
的值(只要写出一组即可);若不存在,说明理由.
【答案】(Ⅰ)见解析
(Ⅱ)![]()
(Ⅲ)![]() ,
,![]() (或
(或![]() )
)
【解析】
(Ⅰ)由题证明![]() (常数)即可证明数列
(常数)即可证明数列![]() 是等差数列;
是等差数列;
(Ⅱ)由(Ⅰ)知![]() ,结合题意在对
,结合题意在对![]() 是奇数和
是奇数和![]() 是偶数分别进行讨论得答案.
是偶数分别进行讨论得答案.
(Ⅲ)由(Ⅰ)知,![]() ,设对任意正整数
,设对任意正整数![]() ,都存在正整数
,都存在正整数![]() ,使
,使![]() ,得
,得![]() ,进而得出答案.
,进而得出答案.
(Ⅰ)∵ ![]() ∴
∴![]() ,
,![]() ,
,
∴ ![]()
化简得:![]() (常数),
(常数),
∴ 数列![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列;
的等差数列;
(Ⅱ)由(Ⅰ)知![]() ,又∵
,又∵![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]()
①当![]() 是奇数时,∵
是奇数时,∵![]() ,∴
,∴![]() ,
,![]()
令![]() ,∴
,∴ ![]()
∵ ![]()
∴ ![]() ,且
,且![]() ,∴
,∴ ![]() ;
;
② 当![]() 是偶数时,∵
是偶数时,∵![]() ,∴
,∴![]() ,
,
令![]() ,∴
,∴ ![]()
∵ ![]()
∴ ![]() ,且
,且![]() ,∴
,∴ ![]() ;
;
综上可得:实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)由(Ⅰ)知,![]() ,又∵
,又∵![]() ,
,
设对任意正整数![]() ,都存在正整数
,都存在正整数![]() ,使
,使![]() ,
,
∴![]() ,∴
,∴ ![]()
令![]() ,则
,则![]() (或
(或![]() )
)
∴![]() (或
(或![]() )
)


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】己知圆![]() :
:![]() 和抛物线
和抛物线![]() :
:![]() ,圆
,圆![]() 的切线
的切线![]() 与抛物线
与抛物线![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() ;
;
(2)设点![]() 为点
为点![]() 关于直线
关于直线![]() 的对称点,是否存在直线
的对称点,是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代在珠算发明之前多是用算筹为工具来记数、列式和计算的.算筹实际上是一根根相同长度的小木棍,如图,算筹表示数1~9的方法有两种,即“纵式”和“横式”,规定个位数用纵式,十位数用横式,百位数用纵式,千位数用横式,万位数用纵式……依此类推,交替使用纵横两式.例如:27可以表示为“![]() ”.如果用算筹表示一个不含“0”的两位数,现有7根小木棍,能表示多少个不同的两位数( )
”.如果用算筹表示一个不含“0”的两位数,现有7根小木棍,能表示多少个不同的两位数( )
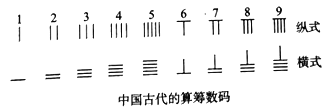
A.54B.57C.65D.69
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C:![]() 1(a>b>0)的离心率为
1(a>b>0)的离心率为![]() ,右准线方程为x=4,A,B分别是椭圆C的左,右顶点,过右焦点F且斜率为k(k>0)的直线l与椭圆C相交于M,N两点(其中,M在x轴上方).
,右准线方程为x=4,A,B分别是椭圆C的左,右顶点,过右焦点F且斜率为k(k>0)的直线l与椭圆C相交于M,N两点(其中,M在x轴上方).
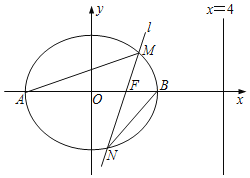
(1)求椭圆C的标准方程;
(2)设线段MN的中点为D,若直线OD的斜率为![]() ,求k的值;
,求k的值;
(3)记△AFM,△BFN的面积分别为S1,S2,若![]() ,求M的坐标.
,求M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中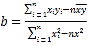 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为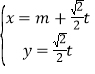 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,椭圆
轴正半轴为极轴建立极坐标系,椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,其左焦点
,其左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求椭圆![]() 的内接矩形面积的最大值.
的内接矩形面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A、B两点的坐标分别为(0,1)、(0,﹣1),动点P满足直线AP与直线BP的斜率之积为![]() ,直线AP、BP与直线y=﹣2分别交于点M、N.
,直线AP、BP与直线y=﹣2分别交于点M、N.
(1)求动点P的轨迹方程;
(2)求线段MN的最小值;
(3)以MN为直径的圆是否经过某定点?若经过定点,求出定点的坐标;若不经过定点,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com