
【题目】在平面直角坐标系xOy中,A、B两点的坐标分别为(0,1)、(0,﹣1),动点P满足直线AP与直线BP的斜率之积为![]() ,直线AP、BP与直线y=﹣2分别交于点M、N.
,直线AP、BP与直线y=﹣2分别交于点M、N.
(1)求动点P的轨迹方程;
(2)求线段MN的最小值;
(3)以MN为直径的圆是否经过某定点?若经过定点,求出定点的坐标;若不经过定点,请说明理由.
【答案】(1)![]() (x≠0).(2)4
(x≠0).(2)4![]() .(3)是,定点(0,﹣2+2
.(3)是,定点(0,﹣2+2![]() )或(0,﹣2﹣2
)或(0,﹣2﹣2![]() ).
).
【解析】
(1)设动点![]() ,再根据斜率之积化简方程即可.
,再根据斜率之积化简方程即可.
(2)分别设![]() 关于的
关于的![]() 的方程,再联立
的方程,再联立![]() 求解
求解![]() 的坐标,进而求得
的坐标,进而求得![]() 关于
关于![]() 的解析式,再利用
的解析式,再利用![]() 化简,利用基本不等式求解最小值即可.
化简,利用基本不等式求解最小值即可.
(3)根据题意可知![]() ,再进行根据
,再进行根据![]() 满足椭圆的方程代入化简求解即可.
满足椭圆的方程代入化简求解即可.
(1)设动点P(x,y),∵A(0,1),B(0,﹣1),
∴直线AP的斜率k1![]() ,直线BP的斜率
,直线BP的斜率![]() ,
,
又k1k2![]() ,∴
,∴![]() ,
,
∴动点P的轨迹方程为![]() (x≠0).
(x≠0).
(2)设直线AP的方程为y﹣1=k1(x﹣0),
直线BP的方程为y+1=k2(x﹣0),
由![]() ,得
,得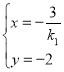 ,∴M(
,∴M(![]() ),
),
由![]() ,得
,得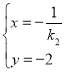 ,∴N(
,∴N(![]() ,﹣2),
,﹣2),
由![]() ,得|MN|=|
,得|MN|=|![]() |=|
|=|![]() |
|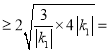 4
4![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
∴线段MN长的最小值为4![]() .
.
(3)设点Q(x,y)是以MN为直径的圆的任意一点,则![]() ,
,
即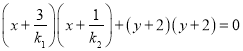 ,
,
又k1k2![]() ,
,
∴以MN为直径的圆的方程为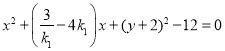 ,
,
令x=0,得(y+2)2=12,解得y=﹣2![]() ,
,
∴以MN为直径的圆过定点(0,﹣2+2![]() )或(0,﹣2﹣2
)或(0,﹣2﹣2![]() ).
).


科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() 且
且![]() .
.
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)若![]() ,且数列
,且数列![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,数列
,数列![]() 满足:
满足:![]() 对于任意给定的正整数
对于任意给定的正整数![]() ,是否存在
,是否存在![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的值(只要写出一组即可);若不存在,说明理由.
的值(只要写出一组即可);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
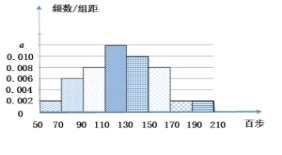
(1)求直方图中a的值,并由频率分布直方图估计该单位职工一天步行数的中位数;
(2)若该单位有职工200人,试估计职工一天行走步数不大于13000的人数;
(3)在(2)的条件下,该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包店推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉.为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:
日需求量 | 15 | 18 | 21 | 24 | 27 |
频数 | 10 | 8 | 7 | 3 | 2 |
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(i)若日需求量为15个,求![]() ;
;
(ii)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地抽查产品进行检测,现在某条生产线上随机抽取100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
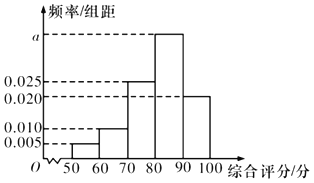
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,以频率作为概率,按分层抽样的思想,先在该条生产线中随机抽取5个产品,再从这5个产品中随机抽取2个产品记录有关数据,求这2个产品中恰有一个一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有一家大型共享汽车公司,在市场上分别投放了黄、蓝两种颜色的汽车,已知黄、蓝两种颜色的汽车的投放比例为![]() .监管部门为了了解这两种颜色汽车的质量,决定从投放到市场上的汽车中随机抽取5辆汽车进行试驾体验,假设每辆汽车被抽取的时能性相同.
.监管部门为了了解这两种颜色汽车的质量,决定从投放到市场上的汽车中随机抽取5辆汽车进行试驾体验,假设每辆汽车被抽取的时能性相同.
(1)求抽取的5辆汽车中恰有2辆是蓝色汽车的概率;
(2)在试驾体验过程中,发现蓝色汽车存在一定质量问题,监管部门决定从投放的汽车中随机地抽取一辆送技术部门作进一步抽样检测,并规定:若抽取的是黄色汽车.则将其放回市场,并继续随机地抽取下一辆汽车;若抽到的是蓝色汽车,则抽样结束;并规定抽样的次数不超过![]() 次,在抽样结束时,若已取到的黄色汽车数以
次,在抽样结束时,若已取到的黄色汽车数以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆方程;
(Ⅱ)设![]() 为椭圆右顶点,过椭圆
为椭圆右顶点,过椭圆![]() 的右焦点的直线
的右焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() ),直线
),直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点. 求证:
两点. 求证:![]() ,
,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com