
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)证明函数![]() 存在唯一的极大值点
存在唯一的极大值点![]() ,且
,且![]() .
.
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是两个不重合的平面,在下列条件中,可判断平面
是两个不重合的平面,在下列条件中,可判断平面![]() ,
,![]() 平行的是( )
平行的是( )
A.![]() ,
,![]() 是平面
是平面![]() 内两条直线,且
内两条直线,且![]() ,
,![]()
B.![]() ,
,![]() 是两条异面直线,
是两条异面直线,![]() ,
,![]() ,且
,且![]() ,
,![]()
C.面![]() 内不共线的三点到
内不共线的三点到![]() 的距离相等
的距离相等
D.面![]() ,
,![]() 都垂直于平面
都垂直于平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为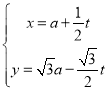 (
(![]() 为参数,
为参数,![]() ).在以坐标原点为极点、
).在以坐标原点为极点、![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的极坐标方程;
的极坐标方程;
(2)已知![]() ,若点
,若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
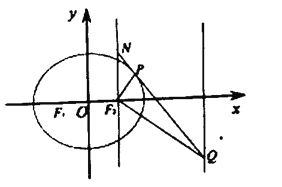
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到
到![]() 的距离之和为4.过点
的距离之和为4.过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试判断直线![]() 与椭圆
与椭圆![]() 公共点的个数,并说明理由;
公共点的个数,并说明理由;
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位运动员一起参加赛前培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:86 85 79 86 84 84 85 91
(Ⅰ)请你运用茎叶图表示这两组数据;
(Ⅱ)若用甲8次成绩中高于85分的频率估计概率,对甲同学在今后的3次测试成绩进行预测,记这3次成绩中高于85分的次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(Ⅲ)现要从中选派一人参加正式比赛,依据所抽取的两组数据分析,你认为选派哪位选手参加较为合适?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
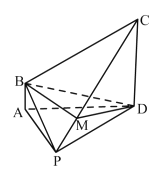
【题目】如图,在四棱锥PABCD-中,AB//CD,AB=1,CD=3,AP=2,DP=2![]() ,PAD=60°,AB⊥平面PAD,点M在棱PC上.
,PAD=60°,AB⊥平面PAD,点M在棱PC上.
(Ⅰ)求证:平面PAB⊥平面PCD;
(Ⅱ)若直线PA// 平面MBD,求此时直线BP与平面MBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面ABCD,底面ABCD为梯形,
底面ABCD,底面ABCD为梯形,![]() ,
,![]() ,且
,且![]() .
.

(1)在PD上是否存在一点F,使得![]() 平面PAB,若存在,找出F的位置,若不存在,请说明理由;
平面PAB,若存在,找出F的位置,若不存在,请说明理由;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com