
| a1+a2+…+an |
| n |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
|


科目:高中数学 来源: 题型:
 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
| A、4 | B、3.15 | C、4.5 | D、3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
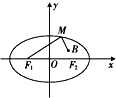 如图,已知椭圆
如图,已知椭圆| x2 |
| 32 |
| y2 |
| 16 |
| MF1 |
| MB |
A、4
| ||
B、6
| ||
| C、4 | ||
| D、6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、人的年龄与其拥有的财富之间具有相关关系 | ||||
| B、从独立性检验可知,在犯错误的概率不超过1%的情况下,有把握认为吃地沟油与患胃肠癌有关系时,我们说某一个人吃地沟油,那么他有99%的可能患胃肠癌 | ||||
| C、从独立性检验可知,在犯错误的概率不超过5%的情况下,有把握认为吃地沟油与患胃肠癌有关系时,是指有少于5%的可能性使得推断吃地沟油与患胃肠癌有关系出现错误 | ||||
D、已知一系列样本点(xi,yi)(i=1,2,3,…,n)的回归直线方程为
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com