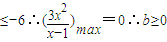【答案】
分析:(I)求出导函数在x=1处的值,利用点斜式写出切线方程,化为斜截式令其斜率为3,纵截距为1,令导函数在-2处的值为0,列出方程组,求出f(x)的解析式.
(II)求出f(x)的导函数,令导函数为0,求出根,列出x,f(x),f′(x)的变化表,求出极大值,端点值,求出函数
f(x)的最大值.
(III)方法一:求出导函数,令导函数大于大于0在区间[-2,1]上恒成立,通过对对称轴与区间位置关系的讨论,求出f′(x)的最小值,令最小值大于等于0,求出b的范围.
方法二:求出导函数,令导函数大于大于0在区间[-2,1]上恒成立,分离出参数b,构造新函数m(x),利用基本不等式求出m(x)的最大值,令b大于等于m(x)的最大值即可.
解答:解(Ⅰ)

(Ⅱ)f'(x)=3x
2+2ax+b=3x
2+4x-4=(3x-2)(x+2)
| x | [-3,-2) | -2 | 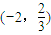 |  | 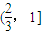 |
| f'(x) | + | | - | | + |
| f(x) | | 极大 | | 极小 | |
f(x)
极大=f(-2)=(-2)
3+2(-2)
2-4(-2)+5=13 f(1)=1
3+2×1-4×1+5=4
∴f(x)在[-3,1]上最大值为13 …(8分)
(Ⅲ)y=f(x)在区间[-2,1]上单调递增
又f'(x)=3x
2+2ax+b,由(1)知2a+b=0∴f'(x)=3x
2-bx+b
依题意f'(x)在[-2,1]上恒有f'(x)≥0,即g(x)=3x
2-bx+b≥0在[-2,1]上恒成立.
①在
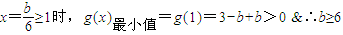
②在

∴b∈
③在
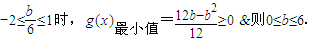
综合上述讨论可知,所求参数b取值范围是:b≥0…(12分)
或者(Ⅲ)y=f(x)在区间[-2,1]上单调递增
又f'(x)=3x
2+2ax+b,由(1)知2a+b=0∴f'(x)=3x
2-bx+b
依题意f'(x)在[-2,1]上恒有f'(x)≥0,即g(x)=3x
2-bx+b≥0在[-2,1]上恒成立∴

令m(x)=3(x-1)+
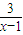
(x≤1)
则m(x)
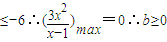 点评:
点评:解决曲线的切线问题时常利用导函数在切点处的值为切线的斜率;解决不等式恒成立常采用分离参数构造新函数,求新函数的最值.


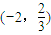

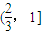
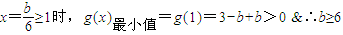
 ∴b∈
∴b∈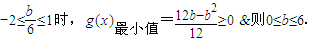

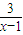 (x≤1)
(x≤1)