
【题目】某保险公司对一个拥有20000人的企业推出一款意外险产品,每年每位职工只要交少量保费,发生意外后可一次性获得若干赔偿金,保险公司把企业的所有岗位共分为![]() 三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
三类工种,从事这三类工种的人数分别为12000,6000,2000,由历史数据统计出三类工种的赔付频率如下表(并以此估计赔付概率):
已知![]() 三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
三类工种职工每人每年保费分别为25元、25元、40元,出险后的赔偿金额分别为100万元、100万元、50万元,保险公司在开展此项业务过程中的固定支出为每年10万元.
(1)求保险公司在该业务所或利润的期望值;
(2)现有如下两个方案供企业选择:
方案1:企业不与保险公司合作,职工不交保险,出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工,企业开展这项工作的固定支出为每年12万元;
方案2:企业与保险公司合作,企业负责职工保费的70%,职工个人负责保费的30%,出险后赔偿金由保险公司赔付,企业无额外专项开支.
请根据企业成本差异给出选择合适方案的建议.
【答案】(Ⅰ)详见解析;(Ⅱ) 方案2.
【解析】试题分析:(Ⅰ)设工种![]() 职工的每份保单保险公司的收益为随机变量
职工的每份保单保险公司的收益为随机变量![]() ,可得其分布列,分别求解数学期望,即可得到该工资的期望值;
,可得其分布列,分别求解数学期望,即可得到该工资的期望值;
(Ⅱ)分别求出方案1和方案2中企业每年安全支出与固定开支,即可作出比较得到结论.
试题解析:
(Ⅰ)设工种A、B、C职工的每份保单保险公司的收益为随机变量X、Y、Z,则X、Y、Z的分布列为
X | 25 |
| |
P |
|
| |
Y | 25 |
| |
P |
|
| |
Z | 40 |
| |
P |
|
| |
保险公司的期望收益为
![]() ;
;
![]() ;
;
![]() ;
;
保险公司的利润的期望值为![]() ,
,
保险公司在该业务所获利润的期望值为9万元.
(Ⅱ)方案1:企业不与保险公司合作,则企业每年安全支出与固定开支共为:
 ,
,
方案2:企业与保险公司合作,则企业支出保险金额为:
![]() ,
,
![]() ,故建议企业选择方案2.
,故建议企业选择方案2.


科目:高中数学 来源: 题型:
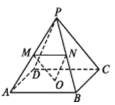
【题目】如图,在棱长均相等的四棱锥![]() 中,
中, ![]() 为底面正方形的中心,
为底面正方形的中心, ![]() ,
,![]() 分别为侧棱
分别为侧棱![]() ,
,![]() 的中点,有下列结论正确的有:( )
的中点,有下列结论正确的有:( )
A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直线![]() 与直线
与直线![]() 所成角的大小为
所成角的大小为![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
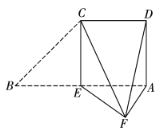
【题目】如图,在直角梯形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,E为AB的中点.将
,E为AB的中点.将![]() 沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为
沿CE折起,使点B到达点F的位置,且平面CEF与平面ADCE所成的二面角为![]() .
.
(1)求证:平面![]() 平面AEF;
平面AEF;
(2)求直线DF与平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
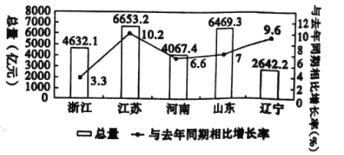
A. 2017年第一季度GDP增速由高到低排位第5的是浙江省.
B. 与去年同期相比,2017年第一季度的GDP总量实现了增长.
C. 去年同期河南省的GDP总量不超过4000亿元 .
D. 2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且
中,O为顶点S在底面ABCD内的投影,P为侧棱SD的中点,且![]() .
.
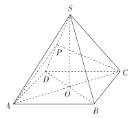
(1)证明:![]() 平面PAC.
平面PAC.
(2)求直线BC与平面PAC的所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级开设了丰富多彩的校本课程,现从甲、乙两个班随机抽取了5名学生校本课程的学分,统计如下表.
甲 | 8 | 11 | 14 | 15 | 22 |
乙 | 6 | 7 | 10 | 23 | 24 |
用![]() 分别表示甲、乙两班抽取的5名学生学分的方差,计算两个班学分的方差.得
分别表示甲、乙两班抽取的5名学生学分的方差,计算两个班学分的方差.得![]() ______,并由此可判断成绩更稳定的班级是______班.
______,并由此可判断成绩更稳定的班级是______班.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com