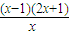己知f(x)=lnx-ax2-bx.
(Ⅰ)若a=-1,函数f(x)在其定义域内不是单调函数,求b的取值范围;
(Ⅱ)当a=1,b=-1时,判断函数f(x)只有的零点个数.
【答案】
分析:(1)已知函数f(x)在其定义域内不是单调函数,所有其导数为0时在定义域内有解,再列出b关于x的式子求解即可.
(2)利用函数在定义域内的单调性和最值研究零点的个数,对f(x)求导,找到单调区间,确定最值f(1)=0,对于?x≠1,f(x)<0,则得到零点个数.
解答:解:(Ⅰ)依题意:f(x)=lnx+x
2-bx,
∵f(x)在(0,+∞)上不是单调函数,∴

,
即b=
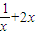
对?x∈(0,+∞)有解,当且仅当
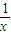
=2x,即x=
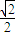
时,
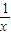
+2x取得最小值2

∴只需b≥2
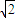
∴b的取值范围为[2

,+∞)
(Ⅱ)当a=1,b=-1时,f(x)=lnx-x
2+x,其定义域是(0,+∞),
∴f′(x)=
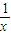
-2x+1=-
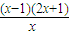
∴当0<x<1时,f′(x)>0;
当x>1时,f′(x)<0
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
∴当x=1时,f(x)取得最大值为0;
当x≠1时,f(x)<f(1)=0,
即f(x)只有一个零点.
点评:利用导数研究函数的单调性,求解函数的单调区间、极值、最值问题,是函数这一章最基本的知识,也是教学中的重点和难点,学生应熟练掌握.

 ,
,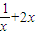 对?x∈(0,+∞)有解,当且仅当
对?x∈(0,+∞)有解,当且仅当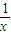 =2x,即x=
=2x,即x=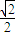 时,
时,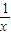 +2x取得最小值2
+2x取得最小值2
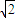
 ,+∞)
,+∞)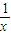 -2x+1=-
-2x+1=-