
����Ŀ������ѧ�ҷ����Ӿ��Ϳռ��������Ա��йأ�Т���л���·������ѧ��ȤС��Ϊ����֤������ۣ�����ȤС���г�ȡ50��ͬѧ����30Ů20����������ͬѧ������ʹ������һ�⣬�ø�λͬѧ����ѡ��һ������н��.ѡ��������±�������λ���ˣ�

��1���ܷ�ݴ��ж���![]() �İ�����Ϊ�Ӿ��Ϳռ��������Ա��й���
�İ�����Ϊ�Ӿ��Ϳռ��������Ա��й���
��2��������������Ů��ѡ���������Ƶ����Ϊ���ʣ��Ӹ�У1500��Ů�������ѡ6��Ů������6��Ů��ѡ�������������Ϊ![]() ����
����![]() ����ѧ����
����ѧ����![]() �ͷ���
�ͷ���![]() .
.
������

�ο���ʽ�� 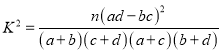 ������
������![]() .
.
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �ϵĵ㵽�����������ľ���֮��Ϊ
�ϵĵ㵽�����������ľ���֮��Ϊ![]() ������Բ
������Բ![]() �Ķ���Ϊֱ����Բ
�Ķ���Ϊֱ����Բ![]() �������������㣬��
�������������㣬��![]() ��
�� ![]() �ֱ�����Բ
�ֱ�����Բ![]() �����Ҷ��㣮
�����Ҷ��㣮
��![]() ����Բ
����Բ![]() ����Բ
����Բ![]() �ķ��̣�
�ķ��̣�
��![]() ����֪
����֪![]() ��
�� ![]() �ֱ�����Բ
�ֱ�����Բ![]() ��Բ
��Բ![]() �ϵĶ��㣨
�ϵĶ��㣨![]() ��
�� ![]() �
λ��![]() �����ࣩ����ֱ��
�����ࣩ����ֱ��![]() ��
��![]() ��ƽ�У�ֱ��
��ƽ�У�ֱ��![]() ��
�� ![]() �ֱ���
�ֱ���![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
�� ![]() ����֤��
����֤�� ![]() Ϊ��ֵ��
Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() ����������
����������![]() ������
������![]() �Ķ�ֱ��
�Ķ�ֱ��![]() ����Բ�ཻ��
����Բ�ཻ��![]() ��������ֱ��
��������ֱ��![]() ��
��![]() ��ƽ��ʱ��ֱ��
��ƽ��ʱ��ֱ��![]() ����Բ
����Բ![]() �صõ��߶γ�Ϊ
�صõ��߶γ�Ϊ![]() .
.
��������Բ![]() �ķ�����
�ķ�����
������![]() �����Ƿ�������ڵ�
�����Ƿ�������ڵ�![]() �Ķ���
�Ķ���![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() �仯ʱ������
�仯ʱ������![]() ���������������
���������������![]() ���������������ڣ���˵������.
���������������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f�䣨x���Ǻ���f��x���ĵ�������f��x����ͼ����ͼ��ʾ����ʽf�䣨x��f��x����0�Ľ⼯Ϊ�� �� 
A.��1��2���ȣ� ![]() ��3���ȣ����ޣ���1��
��3���ȣ����ޣ���1��
B.�����ޣ���1���ȣ� ![]() ��3��
��3��
C.�����ޣ���1���ȣ�3��+�ޣ�
D.��1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������������Ͷ����Ϸ����֪��ÿ��Ͷ�����еĸ��ʾ�Ϊ![]() ����Ͷ��3�ξ�δ���еĸ���Ϊ
����Ͷ��3�ξ�δ���еĸ���Ϊ![]() ����ÿ��Ͷ�����еĸ��ʾ�Ϊ
����ÿ��Ͷ�����еĸ��ʾ�Ϊ![]() ����Ͷ��2��ǡ������1�εĸ���Ϊ
����Ͷ��2��ǡ������1�εĸ���Ϊ![]() ��������ÿ��Ͷ���Ƿ������֮��û��Ӱ��.
��������ÿ��Ͷ���Ƿ������֮��û��Ӱ��.
��1������Ͷ��3�Σ�����������2�εĸ��ʣ�
��2�����ס��Ҹ�Ͷ��2�Σ����������е��ܴ���Ϊ![]() ����
����![]() �ķֲ��к���ѧ����.
�ķֲ��к���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Բ![]() ��
��![]() ������������
������������![]() ����
����![]() �ڶ���
�ڶ���![]() �ϣ���
�ϣ���![]() ��
��
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����![]() Ϊ����ԭ�㣬����
Ϊ����ԭ�㣬����![]() �Ķ�ֱ������Բ����
�Ķ�ֱ������Բ����![]() ���㡣�Ƿ���ڳ���
���㡣�Ƿ���ڳ���![]() ��ʹ��
��ʹ��![]() Ϊ��ֵ�������ڣ���
Ϊ��ֵ�������ڣ���![]() ��ֵ���������ڣ���˵��������
��ֵ���������ڣ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A-BCDE��,����BCDEΪֱ������,CD��ƽ��ABC,����ABCD�ǵ���ֱ��������,��EBC=��ABC=90��,BC=CD=2BE,��M����AD���е�
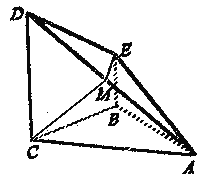
(1)������ֱ��ME��AB���ɽǵĴ�С;
(��)֤��:ƽ��AED��ƽ��ACD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����![]() �Ľ�������Բ
�Ľ�������Բ![]() ��
�� ![]() �Ķ��㣬
�Ķ��㣬 ![]() Ϊ��Բ
Ϊ��Բ![]() ��������Բ
��������Բ![]() ������
������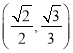 .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������Բ![]() ���Ҷ�����б��Ϊ
���Ҷ�����б��Ϊ![]() ��
��![]() ����ֱ�߽���Բ
����ֱ�߽���Բ![]() ����һ��
����һ��![]() ������
������![]() ���ӳ�
���ӳ�![]() ����Բ
����Բ![]() �ڵ�
�ڵ�![]() ����
����![]() �����ȡ�����ֵʱ����
�����ȡ�����ֵʱ����![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�IJ���ʽa��ax��ex��2x��1����a����1�����ҽ������������⣬��ʵ��a��ȡֵ��ΧΪ�� ��
A.���� ![]() ��
�� ![]() ]
]
B.����1�� ![]() ]
]
C.���� ![]() ����
���� ![]() ]
]
D.���� ![]() ����
���� ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com