
【题目】已知f′(x)是函数f(x)的导函数,f(x)的图象如图所示,则不等式f′(x)f(x)<0的解集为( ) 
A.(1,2)∪( ![]() ,3)∪(﹣∞,﹣1)
,3)∪(﹣∞,﹣1)
B.(﹣∞,﹣1)∪( ![]() ,3)
,3)
C.(﹣∞,﹣1)∪(3,+∞)
D.(1,2)
【答案】A
【解析】解:由f(x)图象单调性可得:
x<﹣1时:,f(x)>0,f′(x)<0,f(x)f′(x)<0;
﹣1<x<0时:f′(x)<0,f(x)<0,f(x)f′(x)>0;
0<x<1时:f′(x)<0,f(x)<0,f(x)f′(x)>0;
1<x<2时:f′(x)>0,f(x)<0,f(x)f′(x)<0;
2<x< ![]() 时:f′(x)>0,f(x)>0,f(x)f′(x)>0;
时:f′(x)>0,f(x)>0,f(x)f′(x)>0;![]() <x<3时:f′(x)<0,f(x)>0,f(x)f′(x)<0;
<x<3时:f′(x)<0,f(x)>0,f(x)f′(x)<0;
x>3时:f′(x)<0,f(x)<0,f(x)f′(x)>0,
∴f(x)f′(x)<0的解集为(0,2)∪(3,+∞).
故选:A.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足![]() 。
。
(1)求证:A,B,C三点共线;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0, ![]() ],函数f(x)=
],函数f(x)=![]() (2m+
(2m+![]() )|
)|![]() |+m2的最小值为5,求实数m的值。
|+m2的最小值为5,求实数m的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】贵阳与凯里两地相距约200千米,一辆货车从贵阳匀速行驶到凯里,规定速度不得超过100千米![]() 时,已知货车每小时的运输成本
时,已知货车每小时的运输成本![]() 以元为单位
以元为单位![]() 由可变部分和固定部分组成:可变部分与速度
由可变部分和固定部分组成:可变部分与速度![]() 千米
千米![]() 时
时![]() 的平方成正比,比例系数为
的平方成正比,比例系数为![]() ;固定部分为64元.
;固定部分为64元.
![]() 把全程运输成本
把全程运输成本![]() 元
元![]() 表示为速度
表示为速度![]() 千米
千米![]() 时
时![]() 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
![]() 为了使全程运输成本最小,货车应以多大速度行驶?
为了使全程运输成本最小,货车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家发现视觉和空间能力与性别有关,孝感市黄陂路高中数学兴趣小组为了验证这个结论,从兴趣小组中抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)以上列联表中女生选做几何题的频率作为概率,从该校1500名女生中随机选6名女生,记6名女生选做几何题的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() .
.
附表:

参考公式: 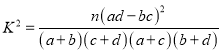 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙H被直线x-y-1=0,x+y-3=0分成面积相等的四个部分,且截x轴所得线段的长为2。
(I)求⊙H的方程;
(Ⅱ)若存在过点P(0,b)的直线与⊙H相交于M,N两点,且点M恰好是线段PN的中点,求实数b的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆中心为坐标原点O,对称轴为坐标轴,且过M(2, ![]() ) ,N(
) ,N(![]() ,1)两点,
,1)两点,
(I)求椭圆的方程;
(II)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆C恒有两个交点A,B,且![]() ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com